Recent Content:
Yesterday I attended the Balancing Act symposium on big data, cybersecurity, and privacy. During the panel discussion, an excerpt from Clarke’s oft-quoted and debatably hyperbolic book on cyber war was invoked:
At the beginning of the era of strategic nuclear war capability, the U.S. deployed thousands of air defense fighter aircraft and ground-based missiles to defend the population and the industrial base, not just to protect military facilities. Every major city was ringed with Nike missile bases to shoot down Soviet bombers. At the beginning of the age of cyber war, the U.S. government is telling the population and industry to defend themselves. As one friend of mine asked, “Can you imagine if in 1958 the Pentagon told U.S. Steel and General Motors to go buy their own Nike missiles to protect themselves? That’s in effect what the Obama Administration is saying to industry today.”
That passage has always struck me as proffering a false equivalence. The US Government has near absolute control over the country’s airspace, and is thereby responsible to defend against any foreign aggression therein. Cyber attacks, on the other hand, are much less overt—with the possible exception of relatively unsophisticated and ephemeral denial of service (DOS) attacks. A typical attacker targeting a private company is most likely interested stealing intellectual property. That’s certainly the trend we’ve seen since the publication of Clarke’s book back in 2012, vi&., Sony, Target, Home Depot, &c. The way those types of attacks are perpetrated is more similar to a single, covert operative sabotaging or exfiltrating data from the companies rather than an overt aerial bombardment.
The actual crime happens within the private company’s infrastructure, not on the “public” Internet. The Internet is just used as a means of communication between the endpoints. More often than not the intermediate communication is encrypted, so even if a third party snooping on the “conversation” were somehow able to detect that a crime were being committed, the conversation would only be intelligible if the eavesdropper were “listening” at the endpoints.
A man has a completely clean criminal record. He drives a legally registered vehicle, obeying all traffic regulations, on a federal interstate highway. A police officer observing the vehicle would have no probable cause to stop him. The man drives to a bank which he robs using an illegal, unregistered gun. Had a police officer stopped the bank robber while in the car, the gun would have been found and the bank robber arrested. Does that give the police the right to stop cars without probable cause? Should the bank have expected the government to protect it from this bank robber?
The only way I can see for the government to provide such protections to the bank, without eroding civil liberties (i.e., the fourth amendment), would be to provide additional security within the bank. Now, that may be well and good in the bank analogy, but jumping back to the case of cyber warfare, would a huge, multi-national company like Sony be willing to allow the US Government to install security hardware/software/analysts into its private network? I think not.
Introduction
In the last post, I presented a new phenomenon called Social Signals. If you have not yet read that post, please do so before reading this continuation. Herein I shall describe the nitty-gritty details of the approach. If you don’t care for all the formalism, the salient point is that we present an unsupervised approach to efficiently detect social signals. It is the approach that achieved the results I presented in the previous post.
The Formal Model (i.e., Gratuitous Math)
We call a measurement of this overall Twitter traffic a baseline. We posit that the signal associated with a bag of words is anomalous for a given time window if the frequency of the words’ usage in that window is uncorrelated with the baseline frequency of Twitter traffic. The aberrance of an anomalous signal is a function of both its frequency and the extent to which it is uncorrelated from the baseline. The significance of an anomalous signal is a function of both its frequency and also the significance of the other abnormal signals to which it is temporally correlated.
Let $\Sigma^*$ be the set of all possible bags of words in a Twitter stream. Let $T \subset \mathbb{N}$ be a consecutive set of points in time that will be used as the index set for the baseline time series, $B = \{B_t : t \in T\}$. Given a bag of words $W \in \Sigma^*$, the associated time series for the signal over the window $T$ is given by $S_W = \{S_{W,t} : t \in T\}$.
The correlation, $\rho : \mathbb{N} \times \mathbb{N} \rightarrow [-1,1] \subset \mathbb{R}$, between two time series, $B$ and $S_W$, is calculated using Pearson’s product-moment correlation coefficient: \begin{multline*} \rho(B, S_W) \mapsto \frac{\mathrm{Cov}\left(B, S_W\right)}{\sigma_B \sigma_{S_W}}\\= \frac{1}{|T|-1}\sum_{i=1}^{|T|} \left(\frac{B_i - \mu_{B}}{\sqrt{\sigma_B}}\right)\left(\frac{S_{W,i} - \mu_{S_W}}{\sqrt{\sigma_{S_W}}}\right), \end{multline*} where $\mathrm{Cov}$ is covariance, $\mu$ is the mean, and $\sigma$ is the standard deviation of the time series. Values of $\rho$ closer to zero indicate a lack of correlation, while values closer to positive and negative one respectively indicate positive and negative correlation. We define the aberrance of a signal with respect to the baseline, $\delta : \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{R}^+$, as the ratio of the signal’s frequency to the magnitude of its correlation to the baseline: $$\delta\left(B, S_W\right) \mapsto \frac{\sum_{t \in T} S_{W,t}}{|\rho(B, S_W)|}.$$
We therefore want to find the set of $n$ signals of maximum aberrance, $\mathcal{S} = \{S_{W_i} : W_i \in \Sigma^*\}$ where $\delta(B,S_{W_1}) \geq \delta(B,S_{W_2}) \geq \ldots \geq \delta(B,S_{W_n})$. Let $\phi : \mathcal{S} \rightarrow \mathcal{S}$ be a convenience function mapping abnormal signals to other abnormal signals to which they are temporally correlated: $$\Big(S_{W_2} \in \phi(S_{W_1})\Big) \implies \left(|\rho(S_{W_1}, S_{W_2})| \geq \frac{1}{2}\right).$$
The significance, $\alpha : \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{R}$, of an abnormal signal $S_W \in \mathcal{S}$ with respect to the baseline is defined recursively: The significance of an abnormal signal is equal to its frequency times the weighted significance of the other abnormal signals to which it is highly temporally correlated. Formally, \begin{multline} \alpha(B, S_W) \mapsto \left(\sum_{t \in T} S_{W,t}\right)\times\\\left(\sum_{S_{W^\prime} \in \phi(S_W)} 2\left(|\rho(S_W, S_{W^\prime})| - \frac{1}{2}\right)\alpha(B, S_{W^\prime}) \right). \label{equ:alpha} \end{multline} Therefore, given the maximally aberrant signals $\mathcal{S}$, we can use the significance function $\alpha$ to provide a total ordering over the signals.
Finally, some signals might be so highly temporally correlated that their bags of words can be merged to create a new, aggregate signal. This can be accomplished by performing clustering on a graph in which each vertex is a signal and edges are weighted according to $\phi$. We have found that this graph is often extremely sparse; simply creating one cluster per connected component provides good results.
Automatically Finding Maximally Aberrant Signals (i.e., The Algorithm)
The model described in the previous section provides a framework in which to find the maximally aberrant signals (i.e., what I was hoping would turn out to be social signals). Creating an algorithm to solve that optimization problem is non-trivial, however. For instance, the recursive nature of the definition of the significance function $\alpha$ requires solving a system of $n$ equations. Fortunately, I was able to identify some relaxations and approximations that make an algorithmic solution feasible. In the remainder of this section, I will describe how I did it.
Given a stream of tweets, a desired time window $T$, and a desired time resolution, the baseline, $B$, and set of signals, $\Sigma^*$, are collected by constructing histograms of term frequency in the tweets for the given time window with bins sized to the desired time resolution. This process is given in Algorithm 1. Since the maximum number of tokens in a tweet is bounded (given Twitter’s 140 character limit), this algorithm will run in $|E|$ time.
| 1: | procedure Collect-Signals($E$, $T$, $\gamma$) |
| Require: $E = \{e_1, e_2, \ldots\}$ is a set of tweets, each being a tuple $\langle \tau_i, \kappa_i\rangle$ containing the timestamp of the tweet, $\tau_i$ and the content of the tweet, $\kappa_i$. $T$ is the desired time window and $\gamma$ is the desired time resolution. | |
| Ensure: $B$ is the baseline measurement and $\Sigma^*$ is the set of possible signals. For all $W \in \Sigma^*$, $S_W$ is the time series for signal $W$. | |
| 2: | $k \gets \frac{|T|}{\gamma}$ /* this is the total number of buckets */ |
| 3: | $B \gets$ an array of $k$ integers, all initialized to zero |
| 4: | $\Sigma^* \gets \emptyset$ |
| 5: | for all $\langle \tau_i, \kappa_i\rangle \in E$ do |
| 6: | if $\tau_i \in T$ then |
| 7: | for all $t \in $ Tokenize$(\kappa_i)$ do |
| 8: | $b \gets \left\lfloor\frac{\tau_i - \inf(T)}{\sup(T) - \inf(T)} k + \frac{1}{2}\right\rfloor$ /* the bucket into which tweet $i$ falls */ |
| 9: | $B[b] \gets B[b] + 1$ |
| 10: | if $\{t\} \notin \Sigma^*$ then |
| 11: | $\Sigma^* \gets \Sigma^* \cup \{\{t\}\}$ |
| 12: | $S_{\{t\}} \gets$ an array of $k$ integers, all initialized to zero |
| 13: | end if |
| 14: | $S_{\{t\}}[b] \gets S_{\{t\}}[b] + 1$ |
| 15: | end for |
| 16: | end if |
| 17: | end for |
| 18: | end procedure |
Next, we need to find $\mathcal{S}$: the set of $n$ signals of maximum aberrance. This can be efficiently calculated in $O\left(|\Sigma^*|\frac{|T|}{\gamma}\right)$ time (for $n$ independent of $|\Sigma^*|$ or $n \ll |\Sigma^*|$), e.g., using the median of medians linear selection algorithm or by using data structures like Fibonacci heaps or skip lists.
The next step is to sort the $n$ maximally aberrant signals in $\mathcal{S}$ by significance. The recursive nature of the definition of the significance function $\alpha$ requires solving a system of $n$ equations. It turns out, however, that the mapping of (\ref{equ:alpha}) is equivalent to the stationary distribution of the distance matrix defined by $\phi$. To see this, first construct a $1 \times n$ vector ${\bf F}$ consisting of the frequencies of the signals: $${\bf F}_i = \sum_{t \in T} S_{W_i, t}.$$ Next, construct an $n \times n$ matrix ${\bf R}$ such that $${\bf R}_{ij} = \begin{cases} 2\left(|\rho(S_{W_i},S_{W_j})| - \frac{1}{2}\right) & \text{if}\ S_{W_j} \in \phi(S_{W_i}),\\ 0 & \text{otherwise.} \end{cases}$$ Let $\hat{\bf R}$ be a normalization of matrix ${\bf R}$ such that the entries of each row sum to one.
The limiting (or stationary) distribution of the Markov transition matrix $\hat{\bf R}$, notated $\boldsymbol{\pi}$, is equivalent to the principal eigenvector (in this case the eigenvector associated with the eigenvalue 1) of $\hat{\bf R}$: $$\boldsymbol{\pi} = \hat{\bf R}\boldsymbol{\pi}.$$ It is a folklore result that $\boldsymbol{\pi}$ can be numerically calculated as follows: \begin{equation} \label{equ:principal} \boldsymbol{\pi} = [\underbrace{1, 0, 0, 0, 0, \ldots}_{n}]\left(\left(\hat{\bf R} - {\bf I}_n\right)_1\right)^{-1}, \end{equation} where ${\bf I}$ is the identity matrix and the notation $({\bf X})_1$ represents the matrix resulting from the first column of ${\bf X}$ being replaced by all ones. Let $C_i$ be the set of states in the closed communicating class (i.e., the set of signals in the connected component of $S_{W_i}$ as defined by $\phi$) of state $i$ in $\hat{\bf R}$. Then, by definition of $\alpha$ in (\ref{equ:alpha}) and by construction of ${\bf F}$ and $\hat{\bf R}$, $$\alpha(B, S_{W_i}) = \pi_i\sum_{j \in C_i}{\bf F}_j.$$
$\boldsymbol{\pi}$ can also be calculated by iterating the Markov process, much like Google’s PageRank algorithm: $$\lim_{k\rightarrow\infty} \hat{\bf R}^k = {\bf 1}\boldsymbol{\pi}.$$ For large values of $n$, this approach will often converge in fewer iterations than what would have been necessary to compute (\ref{equ:principal}). This approach is given in Algorithm 2. If convergence is in a constant number of iterations, the algorithm will run in $O\left({n \choose 2}\right)$ time.
| 1: | procedure Calculate-Significance(${\bf F}, \hat{\bf R}$) |
| Require: $d \in (0,1)$ is a constant damping factor (set to a value of $0.85$). | |
| Ensure: ${\bf A}$ is the resulting significance vector: $\alpha(B, S_{W_i}) = {\bf A}_i$. | |
| 2: | ${\bf A} \gets {\bf F}$ |
| 3: | while ${\bf A}$ has not converged do |
| 4: | ${\bf A} \gets (1-d){\bf A} + d{\bf A}\hat{\bf R}$ |
| 5: | end while |
| 6: | end procedure |
Finally, we want to merge signals that are highly temporally correlated. This is accomplished by clustering the states of the transition matrix $\hat{\bf R}$. We have found that this graph is often extremely sparse; simply creating one cluster per connected component provides good results. An $O(n)$ method for accomplishing this is given in Algorithm 3. Therefore, the entire process of automatically discovering social signals will run in $O\left(|\Sigma^*|\frac{|T|}{\gamma} + n^2\right)$ time.
| 1: | procedure Merge-Signals($\mathcal{S}, \hat{\bf R}$) |
| Ensure: $\mathcal{S}^\prime$ is the set of merged signals. | |
| 2: | $\mathcal{S}^\prime \gets \emptyset$ /* the set of merged signals */ |
| 3: | $s \gets 0$ /* the current aggregate signal index */ |
| 4: | $H \gets \emptyset$ /* a history set to prevent loops when performing a traversal of the graph */ |
| 5: | for $i \leftarrow 1$ to $n$ do |
| 6: | if $i \notin H$ then |
| /* for each signal/vertex that has not yet been traversed */ | |
| 7: | $H \gets H \cup \{i\}$ |
| 8: | $X \gets \{i\}$ |
| 9: | $s \gets s + 1$ |
| 10: | $S^\prime_s \gets \emptyset$ |
| 11: | $\mathcal{S}^\prime \gets \mathcal{S}^\prime \cup \{S^\prime_s\}$ |
| 12: | while $X \neq \emptyset$ do |
| 13: | $j \gets $ Stack-Pop$(X)$ |
| 14: | $S^\prime_s \gets S^\prime_s \cup \{S_{W_j}\}$ /* add signal $S_{W_j}$ to the new aggregate signal $S^\prime_s$ */ |
| 15: | for $k \leftarrow 1$ to $n$ do |
| 16: | if $\hat{\bf R}_{jk} > 0 \wedge k \notin H$ then |
| /* add all of $S_{W_j}$‘s temporally correlated neighbors to the traversal */ | |
| 17: | $H \gets H \cup \{k\}$ |
| 18: | Stack-Push$(X, k)$ |
| 19: | end if |
| 20: | end for |
| 21: | end while |
| 22: | end if |
| 23: | end for |
| 24: | end procedure |
So What?
Social networking sites such as Twitter and Facebook are becoming an important channel of communication during natural disasters. People affected by an event are using these tools to share information about conditions on the ground and relief efforts, as well as an outlet for expressions of grief and sympathy. Such responses to an event in these public channels can be leveraged to develop methods of detecting events as they are happening, possibly giving emergency management personnel timely notifications that a crisis event is under way.
Much of the recent research on addressing this need for event detection has focused on Twitter. Twitter has certain advantages that make it a good model for such research. Among these is the ability to query tweets from a particular location, making it possible to know the geographic location of an emerging event.
Ideally, analysts and first responders would have some system by which they could mine Twitter for anomalous signals, filtering out irrelevant traffic. Twitter does have a proprietary algorithm for detecting “Trending Topics,” however, Twitter’s “Local Trends” feature for identifying trends by geographic region is currently limited to countries and major metropolitan areas (exclusive of cities like Tuscaloosa, Alabama). Furthermore, there is little or no transparency on the specifics of Twitter’s algorithm. It is known that the algorithm relies heavily on rapid spikes in the frequency of usage of a term, therefore biasing toward signals that have broad appeal. An analyst, on the other hand, would be interested in any signal that is abnormal; Twitter’s Trending Topics heuristic might overlook such anomalous signals that have a more gradual increase in frequency.
This work deviates from existing approaches in a number of ways. First and foremost, our approach is based upon a model of a phenomena that was discovered by human analysts that has proven successful for identifying signals specifically related to general events of interest, as opposed to ephemeral topics and memes that happen to have momentarily captured the attention of the collective consciousness of Twitter. Secondly, the proposed approach does not rely on detecting spikes in the frequency or popularity of a signal. Instead, emphasis is placed on detecting signals that deviate from the baseline pattern of Twitter traffic, regardless of the signal’s burstiness. Finally, the proposed approach does not rely on term- or document-frequency weighting of signals (e.g., tf-idf), which can be troublesome for short documents (e.g., tweets) because signals’ weights will be uniformly low and therefore have very high entropy, i.e., the probability of co-occurrence of two terms in the same tweet is extremely low, especially if the number of documents is low. Since we are not characterizing signal vectors for individual tweets, we can examine the frequencies of individual signals independently. In a sense, we treat the entire stream of tweets as a single document.
Once again, many thanks to my collaborators, Clay Fink and Jaime Montemayor, without whom this work would not have been possible.
Social Signals
or, the basis for an article that was nominated for best paper and subsequently rejected.
Introduction
Looking back on my previous job at The Johns Hopkins University, I am struck by and grateful for the breadth of different topics I was able to research: distributed phased array radar resource scheduling, Linux kernel integrity monitoring, TLS, hypervisors, probabilistic databases, streaming algorithms, and even some DNA sequencing, just to name a few.
Toward the end of my—to abuse an overloaded term—tenure at JHU/APL, I became involved in their social media analysis work. For example, I had some success creating novel algorithms to rapidly geolocate the context of social media posts, based solely upon their textual content. But one of the most interesting things I encountered along these lines was a phenomena that we came to call Social Signals.
Discovery of Social Signals
As will become evident from the following chronology, I was not party to this line of research until after many of the initial discoveries were made, so my account of the earlier details may be inaccurate. To my knowledge, however, this is the first time any of these discoveries have been made publicly available in writing.
In 2011, my colleague Clay Fink had been mining Twitter for tweets for quite some time. He had gigabytes of them, spanning months and covering various worldwide events like the London riots, the Mumbai bombings, the Tuscaloosa—Birmingham tornado, the Christchurch earthquake, the Nigerian bombing, &c. These provided a very interesting and, as it turned out, fruitful source of data to research. They shared the common theme of being crises, yet they were each of a very different nature, e.g., some were man-made and others natural disasters.
Clay had created some algorithms to process the mass of textual data, but there was no good, usable way for a human to sift through it to do manual analysis. Step in another colleague, Jaime Montemayor, who created a data exploration tool called TweetViewer.
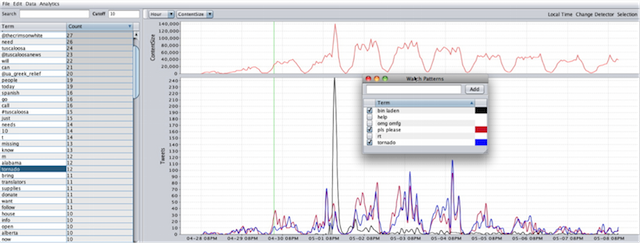
TweetViewer is very simple in concept: It plots the relative term frequencies used in a text corpus over time. Yet this simple concept—coupled with the algorithms and HCI workflow accelerators (as Jaime calls them) behind-the-scenes that allow real-time interaction with and instantaneous feedback from the data—enabled some interesting disoveries. Take the large spike in Twitter traffic around May 2nd as an example: it corresponds to the killing of Osama bin Laden—the event associated with the highest sustained rate of Twitter traffic up to that point. Selecting the term “bin Laden” instantly generates its time series in the lower graph, which correlates perfectly with the spike in overall traffic.
This example perfectly illustrates one of the challenges of social media analytics, for there were three other major events being concurrently discussed on Twitter that were masked by the popularity of the bin Laden killing: the British royal wedding, a $100k fine levvied on Kobe Bryant, the NBA finals, and a tornado that devastated several cities in the Southern United States. Monitoring "trending topics" based upon spikes in the frequency or popularity of terms would not detect these less popular topics of discussion.
By exploring Clay's corpora in TweetViewer, he and Jaime quickly noticed a pattern: there were certain terms that always seemed to spike in frequency during a crisis event. These included "help," "please," and "blood," as well as various profanities. In the Nigerian bombing corpora, for example, there was a large spike in Twitter traffic temporally correlated with the bomb explosion, and a subsequent spike minutes later correlated with a bomb scare (but no actual blast). The frequency timeseries for the term "blood" pefectly correllates to the actual bomb blast, but does not spike again during the bomb scare. Clay and Jaime dubbed these terms Social Signals.
Automating the Process
When I was first briefed on this phenomenon I was immediately intrigued, primarily around the potential of publishing an academic paper peppered with legitimate use of profanity.
…
Nam castum esse decet pium poetam
ipsum, versiculos nihil necessest;
…
The challenge was that these social signals were discovered by humans. Were there others we had missed? Would this phenomenon extend to languages other than English? Could an algorithm be designed to classify and track social signals?
I played around with the data in TweetViewer for a while, and I eventually developed a theory as to what made a term a social signal. My underlying hypothesis was that the human-identified social signals are a subset of a larger class of abnormal terms whose frequency of usage does not correlate with the overall frequency of Twitter traffic. For each geographic region, Twitter traffic ebbs and flows in a pattern much like a circadian rhythm. In the Twitter posts captured from the Tuscaloosa tornado event, for example, traffic peaks around 23:00 every night and then rapidly falls—as people go to sleep—and reaches a nadir at about 09:00—when people are arriving at work. It is actually very regular, except for when people are discussing an unexpected event.
As an example, consider the terms "please" and "blood," which we have observed to temporally co-occur with certain types of disaster events. Under normal circumstances these terms are not temporally correlated to each other; however, during a disaster scenario they are. Furthermore, the term "blood" does not have a very high frequency, so methods based strictly on the frequency domain or burstiness of the terms might ignore that signal. Therefore, we first identify the set of maximally abnormal term signals, vi&., those that are temporally uncorrelated with the overall Twitter traffic. Next, these abnormal signals are sorted according to a significance metric which is based on how temporally correlated they are to each other. Finally, an unsupervised graph clustering algorithm is used to merge similar signals.
For the sake of brevity, I am going to save the technical details for a later post. I will likely also be publishing a related manuscript on the arXiv.
Results
We evaluated our approach on a number of Twitter datasets captured during various disaster scenarios. The first corpus we examined includes tweets from the April 2011 tornados in Tuscaloosa, Alabama. This is the interesting corpus mentioned above in which the tornados co-occurred with the British Royal wedding, a much discussed $100,000 fine of NBA player Kobe Bryant, and the killing of Osama bin Laden—the event associated with the highest sustained rate of tweets per second to date. The second corpus includes tweets from the February 2011 earthquake in Christchurch, New Zealand. The final corpus includes tweets leading up to and including the July 2011 bombings in Mumbai, India. This corpus is interesting because it includes tweets from the prior thirteen days leading up to the bombings.
The time bucket size was set to 20 minutes. The number of maximally aberrant signals discovered was 300. For each corpus, the resulting automatically detected signals included the human-identified social signals “help” and “please.” The Mumbai corpus also included the “blood” social signal. The clustered signals of highest significance are given in the following table, in which green signals are ones that are clearly related to an important event:
| Dataset | Start Date | End Date | # Tweets | # Terms |
|---|---|---|---|---|
| Tuscaloosa | April 28, 2011 15:46:35 CDT | May 8, 2011 21:43:48 CDT | 97409 | 58232 |
Top Detected Signals (sorted by decreasing significance)
tuscaloosanews greek relief need disaster followers text tell redcross like needs just back alabama tornado laden osama news dead obama know tuscaloosa really come thanks will help youtube helpttown right right love lakers think supplies mothers mother happy first volunteers give spann time donation make donate please courtside tickets
|
||||
| Christchurch | February 17, 2011 23:10:03 NZDT | February 24, 2011 11:51:11 NZDT | 12973 | 15223 |
Top Detected Signals (sorted by decreasing significance)
need safe #eqnz earthquake still people know help please chch family anyone christchurch will quake #chch jobs #job canstaff victims darkest donate zealand towards donation make redcross just today power thanks everyone news home thank water christchurchcc open yeah tumblr photo another bexielady haha dairy nzne wellington nzpa #christchurch want
|
||||
| Mumbai | July 1, 2011 21:39:06 IST | July 15, 2011 03:29:30 IST | 164820 | 123516 |
Top Detected Signals (sorted by decreasing significance)
need govt terror good every people varsha love twitter thanks hear time help please police anybody says serious right work control mumbai karia going think blood like #mumbai injured kasab will even make hospital room blasts stop home call parents blast today well looking life india dadar want just safe #mumbaiblasts stay news rahul come indian #here back know take anyone spirit also #bse #stocks #tips turn following sexy #instantfollow bitch #images #india #free
|
||||
The Aftermath
Excited that we had developed an automated, completely unsupervised, language-agnostic technique for detecting social signals—which also happened to detect the same signals discovered by human analysis—we quickly wrote up a paper and submitted it to a conference. A few months later the reviews came back:
Reviewer 1
Accept Nominate for Best Paper
Reviewer 2
Accept
Reviewer 3
Reject
As you might have guessed, the paper was ultimately rejected.

Shortly after, I left JHU and didn’t continue this line of research, so it’s just been bit-rotting for the past few years.
In summary, our paper introduced the discovery of social signals: elements of text in social media that convey information about peoples’ response to significant events, independent of specific terms describing or naming the event. The second contribution of the paper was a model of the mechanisms by which such signals can be identified, based on the patterns of human-identified signals. Finally, a novel unsupervised method for the detection of social signals in streams of tweets was presented and demonstrated. For a set of corpora containing both natural and human-caused disasters, in each instance our model and algorithms were able to identify a class of signals containing the manually classified social signals.
Future work includes optimizing the algorithms for efficiency in processing streaming Twitter traffic. Incorporating estimates of provenance and trustworthiness from the Twitter social network, as well as accounting for the propagation of signals through re-tweets, might improve the relevance of the detected signals. Finally, we hoped to perform a sensitivity analysis of the algorithms by detecting signals across domains, e.g., using a baseline from one disaster-related event to detect signals during a similar event at a different time.
Success in OS X
10 easy steps (and lots of unnecessary prose) on how to set up a new PowerBook in 48 hours or more.
Five years ago I wrote about my travails solving some networking issues on my Linux laptop. I equated the experience to a classic XKCD comic in which a simple software fix escalates to a life-and-death situation. The same thing happened to me again, this time on Mac OS X.
For those who weren’t aware, I recently moved from Washington, D.C. to Philadelphia. I still work in DC, though; it’s about a two-hour commute door-to-door, during the majority of which I am able to do work while on the train. My old commute was a minimum of 45 minutes by car, during which I could not work, so my unproductive time has actually decreased. I also joke with some of my colleagues who live further afield in Virginia that my commute is often shorter than theirs, thanks to the terrible D.C. traffic. A single accident on the beltway and my commute across four states is shorter than their ~20-mile drive.
I am currently working a project at a customer site in Northern Virginia. It’s a bit of a pain to get to without a car, but I put up with it because the project will be wrapping up sooner than later. Monday morning I arrived, ready to start work, and I open my laptop to check my mail before heading into the lab. I wake the computer up from its sleep and the screen is frozen. That’s not entirely alarming, since hibernation and sleep are still tricky, bug-prone processes, even on modern operating systems. So, I hard-reboot the laptop. The initial password prompt to decrypt my hard drive comes up, but the screen is all striated with weird, interlacing-like artifacts. My mouse and keyboard appear to still work, however, so I try and log in. It works, and the boot progress bar proceeds as normal. About half-way through the boot process, the screen abruptly goes black and the computer restarts itself.
Huh.
I hard-reboot and try again. Same thing. Zap the PRAM (an act I had completely forgotten about since the ‘90s, the last time I had to use it). Same thing. Booting into safe mode? Same thing.
At this point, I’m worried that it’s my hard drive. I’ve had countless hard drive failures throughout my computing career, and they’re never fun. But I try booting into single-user mode, and that works perfectly, suggesting that it might not be a hard drive problem after all. I can mount the hard drive just fine, and all the files appear intact. I keep regular backups, so the only data I would stand to lose would be the work I did earlier that morning on the train down. Not a big deal, and I could always retrieve it by going into single-user mode. The trouble now is that if this truly is a hardware issue, the fix would likely be buying a new laptop as opposed to buying a replacement hard drive.
I am in the Northern Virginia suburbs with no car and no ability to communicate, let alone do work, other than on my phone.
I shoot out a few E-mails on my phone and head into the lab.
I try and log onto a desktop in the lab. It accepts my user credentials, but the screen then just goes black. So I walk over to one of the administrators and ask,
Is everything okay with the domain controller? I’m having trouble logging in.
Oh … yeah … well, we just had a switch inexplicably brick itself, and one of our servers died, too.
I recently finished reading Bleeding Edge (which contains the most faithful representation of the late ‘90s hacker culture I have ever encountered in fiction), and I am currently ¾ of the way through Pynchon’s previous novel, Inherent Vice (the film adaptation of which is currently in theaters). Both books share similar themes and plotlines centered around conspiracy theories, paranoia, the government, three-letter agencies, electromagnetic pulse weapons meant to destroy electronics, and (D)ARPA.
So, here I am, inside the D.C. beltway, sitting in a nondescript office building owned by a government contractor, surrounded by SCIFs in which work on classified DARPA projects is undoubtedly being carried out, and three different hardware devices inexplicably and simultaneously fail. I’ll be honest, I start freaking out a little. I tell the administrators that my laptop failed at the same time, and they start to get a bit paranoid, too.
…in the business, paranoia was a tool of the trade, it pointed you in directions you might not have seen to go. There were messages from beyond, if not madness, at least a shitload of unkind motivation.
Paranoia’s the garlic in life’s kitchen, right, you can never have too much.
In the late ‘90s, back when I was working at a commercial software company, we got a call from a customer who had received our product just a week earlier. It had stopped working, to the extent that the server couldn’t even boot. We retrieved the server, found that the operating system had been corrupted, reinstalled everything, and gave it back. One week later, the exact same thing happened again. And again. It turned out that the customer’s server room shared a wall with the dentist’s office next door, and the X-ray machine was pointed directly at the server. Every time the X-ray was fired, some bits would randomly get flipped on the hard drive.
Was I being irradiated every time I went to this D.C. job site? Was it a freak solar flare? An electromagnetic burst? Something more nefarious? I’ll probably never know.
If there is something comforting—religious, if you want—about paranoia, there is still also anti-paranoia, where nothing is connected to anything, a condition not many of us can bear for long.
Back in meatspace, Nate comes to my rescue. He picks me up, drives me to the closest BestBuy, and we buy a replacement MacBook. (The price at BestBuy was actually several hundred dollars cheaper than if we had bought it direct from Apple.) Unfortunately, the only laptops in stock have smaller hard drives than the laptop I am replacing. I figured I’d just get an external hard drive to store my VMs and call it a day.
That night, back home in Philly, I open the tidy Apple packaging of the new laptop and start setting it up. I go to connect the external hard drive on which I have my backup, and I realize that I had been connecting it to my old laptop using a FireWire 800 cable. The new laptop, however, only has USB and Thunderbolt. The hard drive fortunately does support (now antiquted) USB 2.0, through a full-size male-to-male connector. Who has full-size USB cables anymore? Everything these days is either mini or micro. I call a few stores and no one has them in stock. Begrudgingly, I embark on my second trip to BestBuy in five years.
On my way to the store, I glimpse out of the corner of my eye the distinctive signage of a RadioShack. Perhaps this one hasn’t been closed yet? I am suddently swept with an emotion for which no single word in English suffices; perhaps what the Portuguese would call saudade. An “Ubi sunt nunc?” sort of thing.
♬♬♬♬
Why are you leaving the party so early,
Just when it was getting good?
Were the crowds and the laughter just a little too tame,
Did the girl you had your eye on go and forfeit the game?
O tell me
Where is there music any gayer than ours, and tell me
Where are wine and ladies in such ample supply?
If you know a better party in the Southwest Protectorate,
Tell us and we’ll drop on by
(Right after this one)
Tell us and we’ll drop on by.
♬♬♬♬
The RadioShack is in an area of the city I’m unfamiliar with, but it’s on my way to BestBuy, so it’s not a detour. I decide to swing by. I hadn’t been to a RadioShack in years, and I’d rather give my money to them. I drive in the direction of where I thought I saw the sign. Only a strip-mall with a toystore. I whip out my phone and search for “RadioShack.” Google Maps doesn’t report anything. Google search doesn’t report anything.
Of course, in NYC it is not uncommon to catch sight of a face that you know, beyond all argument, belongs to somebody no longer among the living, and sometimes when it catches you staring, this other face may begin to recognize yours as well, and 99% of the time you turn out to be strangers.
BestBuy, undoubtedly knowing the cord’s scarcity, sells them for \$25 at what must be a 5000% markup.

That’s right, it has “pre-installed software on the cable”!
Back home, at 9 PM, I am finally able to start the restore from backup. It’s slow, thanks to the USB 2.0, but it’s working. By midnight, all of my documents and system settings are 20 minutes away from being completely transferred. Next step is to transfer the applications. I go to sleep and let it work overnight.
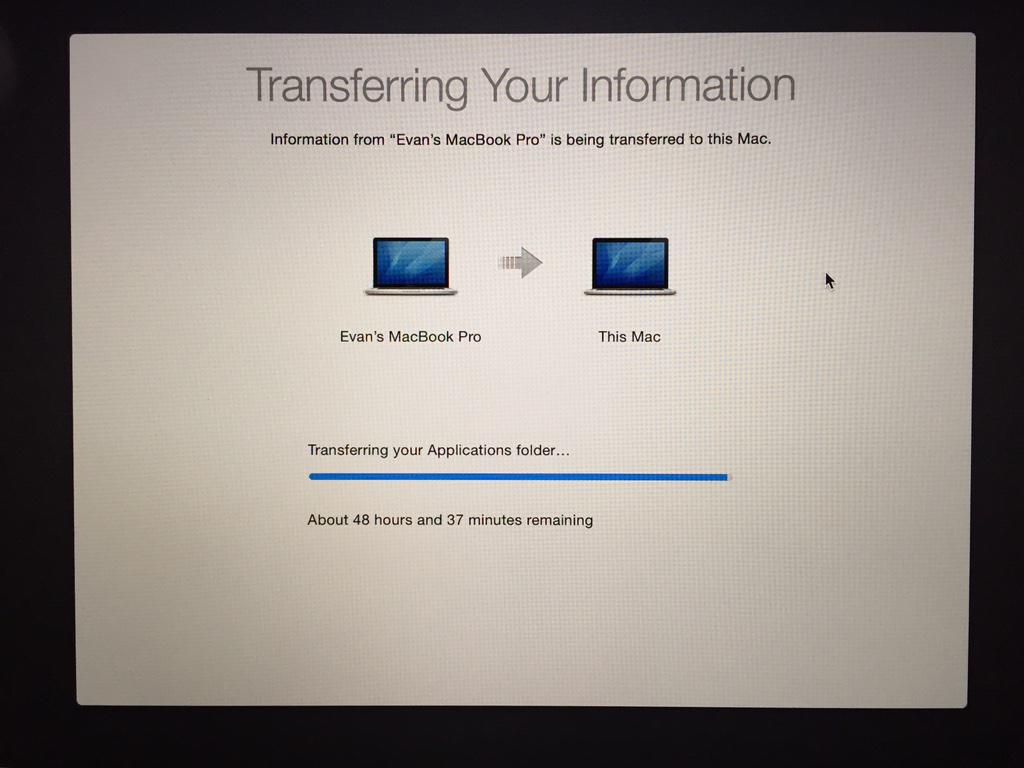
The next morning I wake up to this:
48 hours to go.
The time remaining is wildly fluctuating, jumping by hours at a time, so I decide to wait a bit in the hopes that it is just a glitch in the time estimation calculation. Perhaps the laptop went into powersaving sleep mode after I fell asleep, and the multi-hour lull in progress is confusing it?
Four hours later, when the estimated time remaining has crept to 400 hours, I call it quits and shut down the machine.
Before attempting to do the restore again, I search the Internet for anyone else who’s had this problem and, sure enough, the trail has been blazed with the frustrations of others. One option that worked for someone else was to reboot into recovery mode and completely reinstall the drive from the backup (as opposed to migrating my documents, settings, and applications into the OS install that shipped with the new laptop). This isn’t ideal, because it clones the entire OS from my old laptop (which had different hardware), and if the laptop’s failure were due to problems in software, those problems might be inherited by the new laptop. I decided to proceed, as it seemed to work for random-Internet-dude.
I step through the process of doing a complete restore from the backup. It warns me that everything currently on the drive will be deleted. Sure. It asks if I want my hard drive to be fully encrypted. Yes, please. Finally, just before it starts, it tells me that my new hard drive isn’t big enough to do a full restore.
Back to the drawing board.
I have multiple advanced degrees in Computer Science. What chance would the “laity” have?
“…every day civilians walk around, no clue, even when it’s filling up screens right next to them at Starbucks, cyberspace warfare without mercy, 24/7, hacker on hacker, DOS attacks, Trojan horses, viruses, worms…”
At this point, my only other option is to reset the OS to factory settings, start a data migration from my TimeMachine backup as I did before, yet this time select to transfer everything except applications. I’ll just have to manually install all of my applications later.
The OS is definitely in a weird state, though, since I shut down the computer in the middle of the failed migration. Plus, who knows what happened when I tried to restore from the too-large backup? So, reading some instructions online, I decide that I need to completely wipe the hard drive, reinstall OS X, and then use the setup assistant again to do the application-less migration.
I boot up into restore mode, open up DiskUtility, and erase the main hard drive partition. It gets erased, alright, but now DiskUtility is no longer able to do anything to the logical drive: I can’t reformat/erase it or anything. It’s visible, but all the options are greyed out. It is there, yet inaccessible.
They gaze at each other for a while, down here on the barroom floor of history, feeling sucker-punched, no clear way to get up and on with a day which is suddenly full of holes—family, friends, friends of friends, phone numbers on the Rolodex, just not there anymore … the bleak feeling, some mornings, that the country itself may not be there anymore, but being silently replaced screen by screen with something else, some surprise package, by those who’ve kept their wits about them and their clicking thumbs ready.
Once again, thanks to some anonymous Internet trailblazers, I
discover that selecting to encrypt my hard drive on the earlier
attempts caused the OS to format the drive using CoreStorage, which is
not yet supported by DiskUtility. So, after the long and annoying process of creating a Yosemite
USB boot drive (which it turns out may not have even been
necessary), I am able to get a terminal on which I can enter the
requisite incantation of diskutil cs delete "Macintosh
HD" to fix my partition.
I then reinstall OS X and—24 hours after I bought the laptop—I am able to get it back to a factory state. I start the data migration (minus applications). Several hours later, I have a functioning, application-less system.
The next day, I take apart the old computer and remove the hard drive. Even without the hard drive, it boots to a screen with corrupted video, indicating that there is at least some hardware problem unrelated to the hard drive.
He that we last as Thurn and Taxis knew
Now recks no lord but the stiletto’s Thorn,
And Tacit lies the gold once-knotted horn.
No hallowed skein of stars can ward, I trow,
Who’s once been set his tryst with Trystero.
The moral of the story is: Back up your files, only upgrade to a computer if it has a larger hard drive than your previous one, stay away from electromagnetic pulses, and chill out, man.
Though hardly a connoisseur of the freakout, he did recognize a wraparound hallucination when he saw one…W.A.S.T.E.
For as long as I’ve understood object-oriented programming, I’ve had an ambivalent relationship with C++. On the one hand, it promised the low-level control and performance of C, but, on the other, it also had many pitfalls that did not exist in other high-level managed languages like Java. I would often find myself in a position where I wouldn’t be sure exactly what the compiler would do under-the-hood. For example, when passing around objects by value would the compiler be “smart” enough to know that it can rip out the guts of an object instead of making an expensive copy? Granted, much of my uncomfortableness could have been remedied by a better understanding of the language specification. But why should I have to read an ~800 page specification just to understand what the compiler is allowed to do? The template engine and the STL are incredibly powerful, but it can make code just as verbose as Java, one of Java’s primary criticisms. Therefore, I found myself gravitating toward more “purely” object-oriented languages, like Java, when a project fit with that type of abstraction, and falling back to C when I needed absolute control and speed.
A couple years ago, around the time when compilers started having
full support for C++11, I started a project that was tightly coupled
to the LLVM codebase,
which was written in C++. Therefore, I slowly started to learn about
C++11’s features. I now completely agree with Stroustrup: It’s best to think of C++11 like a completely new
language. Features like move
semantics give the programmer complete control over when the
compiler is able to move the guts of objects. The new auto type deduction keyword gets rid of a
significant amount of verbosity, and makes work with complex templates
much easier. Coupled with the new decltype keyword, refactoring object member
variable types becomes a breeze. STL threads now make porting concurrent code much
easier. That’s not to mention syntactic sugar like ranged for statements, constructor inheritance,
and casting keywords. And C++ finally has lambdas! C++11 seems to be a bigger leap forward
from C++03 than even Java 1.5 (with its addition of generics) was
to its predecessor.
As an example, I recently needed an unordered hash map where the keys were all pointers. For example,
std::unordered_map<char*,bool> foo;I wanted the keys to be hashed based upon the memory addresses of the character pointers, not the actual strings. This is similar to Java’s concept of an
IdentityHashMap. Unfortunately, the
STL does not have a built-in hash function for pointers. So I created one thusly:
/* for SIZE_MAX and UINTPTR_MAX: */
#include <cstdint>
namespace hashutils {
/* hash any pointer */
template<typename T>
struct PointerHash {
inline size_t operator()(const T* pointer) const {
auto addr = reinterpret_cast<uintptr_t>(pointer);
#if SIZE_MAX < UINTPTR_MAX
/* size_t is not large enough to hold the pointer's memory address */
addr %= SIZE_MAX; /* truncate the address so it is small enough to fit in a size_t */
#endif
return addr;
}
};
}
Note that I am using auto here to reduce verbosity, since it is evident that addr is a uintptr_t from the righthand side of the assignment.
The hashutils::PointerHash object allows me to do this:
std::unordered_map<char*,bool,hashutils::PointerHash<char>> foo;The neat part is that C++11 has a new
using keyword that essentially lets me generically alias that definition:
template<typename K,typename V> using unordered_pointer_map = std::unordered_map<K,V,hashutils::PointerHash<typename std::remove_pointer<K>::type>>; unordered_pointer_map<char*,bool> foo;Note the use of
std::remove_pointer<_>, a great new
STL template that gets the base type of a pointer.
In another instance, I wanted to have a hash map where the keys were pointers, but the hash was based off of the dereferenced version of the keys. This can be useful, e.g., if you need to hash a bunch of objects that are stored on the heap, or whose memory is managed outside of the current scope. This, too, was easy to implement:
namespace hashutils {
template<typename T>
inline size_t hash(const T& v) {
return std::hash<T>()(v);
}
/* hash based off of a pointer dereference */
template<typename T>
struct PointerDereferenceHash {
inline size_t operator()(const T& pointer) const {
return hash(*pointer);
}
};
/* equality based off of pointer dereference */
template<typename T>
struct PointerDereferenceEqualTo {
inline bool operator()(const T& lhs, const T& rhs) const {
return *lhs == *rhs;
}
};
template<typename K,typename V>
using unordered_pointer_dereference_map = std::unordered_map<K,V,PointerDereferenceHash<K>,PointerDereferenceEqualTo<K>>;
}
Note that, through the magic of the C++ template engine, this code
supports keys that are pure pointers as well as C++11’s new smart pointers.
As another example of the afforementioned auto keyword
and ranged for statements, this is how easy it is in C++11 to hash an
entire collection (e.g., a std::vector or
std::set):
namespace hashutils {
class HashCombiner {
private:
size_t h;
public:
HashCombiner() : h(0) {}
template <class T>
inline HashCombiner& operator<<(const T& obj) {
/* adapted from boost::hash_combine */
h ^= hash(obj) + 0x9e3779b9 + (h << 6) + (h >> 2);
return *this;
}
operator size_t() const { return h; }
};
/* hash any container */
template<typename T>
struct ContainerHash {
size_t operator()(const T& v) const {
HashCombiner h;
for(const auto& e : v) {
h << e;
}
return h;
}
};
}
Then, to make all sets hashable (and thereby valid to be used as keys in a map), simply add this:
namespace std {
template<typename... T>
struct hash<set<T...>> : hashutils::ContainerHash<set<T...>> {};
}
I realize that this post is a collection of rather mundane code snippets that are nowhere near a comprehensive representation of the new language features. Nevertheless, I hope that they will give you as much hope and excitement as they have given me, and perhaps inspire you to (re)visit this “new” language called C++11.
Seven months ago I asked the following question on StackExchange:
Sometimes, when I have many applications open doing many memory and IO-intensive things, my computer inevitably starts to thrash a bit. While waiting for things to settle down, I often decide to close some applications that don’t really need to be open. The trouble is that many of the applications (especially ones that have background/idle processes) tend to be intermittently unresponsive until the thrashing subsides, so it either takes a very long time for them to get focus to send ⌘+q, or when I go to close them by clicking on their icon in the dock I am only presented with the option to force quit. I know that those applications aren’t permanently unresponsive, so I’d prefer to send them a gentle TERM signal and have them quit gracefully when they are able. I usually end up killing them by using
pkillfrom the terminal, however, that’s not always feasible, especially if the terminal is also hosed.What is the easiest way to gently send the signal to kill a process if/when that process is intermittently unresponsive? (In a situation in which access to the terminal and/or starting a new application is not convenient.)
The question didn’t get much fanfare on StackExchange, and the only
answer so far has been to use AppleScript to essentially
programmatically send the ⌘+q signal to the
application. I’ll bet it’s basically equivalent to using
pkill from the terminal to send a SIGTERM to the
process, but it might work in the event that my terminal emulator app
is also unresponsive. Anyhow, it was the best solution I had, so I
matured the idea by making a friendly standalone AppleScript that
enumerates all of the currently running processes and prompts the
users for which to gently kill. Here it is:
local procnames
tell application "System Events"
set procnames to (get the name of every process whose background only is false and name is not "GentleKill")
end tell
(choose from list procnames with prompt "Which applications would you like to gently kill?" with multiple selections allowed)
if result is not false then
set tokill to result
set text item delimiters to {", "}
display dialog "Are you sure you want to gently kill " & tokill & "?"
repeat with prog in tokill
tell application prog to quit
end repeat
end if
Steamed fish that is finished with a drizzle of hot oil is a classic Cantonese dish. The way I like to make it includes a few Japanese ingredients, and my method is a bit unorthodox.

Hardware
- 12 inch frying pan with lid
- A small raised rack that will fit inside the pan that can provide a centimeter or so of clearance above the bottom of the pan; the removable rack that came with my toaster oven works perfectly
- A very small bowl
- A small saucepan (it can be tiny)
- A platter for serving that is large enough for the fish and deep enough to hold some sauce
Software
- 2 tbsp. soy sauce
- 1 tbsp. mirin
- 1 tbsp. shaoxing cooking wine, or you can substitute an additional tbsp. of mirin
- 1 tbsp. sake
- 1/4 cup of either water, katsuo dashi stock, or water plus half of an instant dashi stock packet
- 1 fillet of a large flaky fish. Approximately 1 pound. I often use rockfish or wild striped bass. If you cannot find a large fillet, a smaller whole fish can be used.
- 1/4 cup coarsely chopped cilantro
- 2 in. knob of ginger, peeled and julienned
- 2 scallions, both whites and greens, julienned (or thinly sliced at an oblique angle, similar to the thicker Chinese “horse ear” cut)
- hot chili pepper, sliced thin at an oblique angle (optional)
- 1/8 tsp. five spice powder
- 1/4 tsp. toasted sesame oil
- 2 tbsp. vegetable oil
Algorithm
- Mix the soy sauce, mirin, shaoxing wine, sake, and water/dashi in the frying pan
- Place the fish into the pan and marinade for 15 minutes, flipping once half way
- Meanwhile, combine the ginger, cilantro, scallion, optional chili pepper, five spice and toasted sesame oil in a small bowl and mix
- Remove the fish from the marinade, place the rack into the pan, and the fish onto the rack
- Bring to a boil
- Once boiling, cover the pan tightly, reduce the heat to simmer, and steam for 8 minutes
- Meanwhile, start heating the vegetable oil in the small saucepan
- When the fish is done steaming, remove it and the rack from the pan, placing the fish on the platter
- Increase heat to high and let the sauce reduce to the consistency of Grade A (runny) maple syrup
- Pour the sauce over the fish and put the herb mixture on top of the fish
- When the vegetable oil is very hot, spoon it over top of the herbs
 PoC‖GTFO
PoC‖GTFO Twitter
Twitter LinkedIn
LinkedIn GitHub
GitHub XTerm
XTerm
 English
English
 עברית
עברית
 Medžuslovjansky
Medžuslovjansky
 Русский
Русский


 Reply
Reply Retweet
Retweet Favorite
Favorite