Recent Content:
Sir Robert Burnett
An investigation into the life of the patron saint of alcoholic graduate students.
Political scientist Ed Burmila—sole remaining contributor to one of my favorite weblogs on the Internets, Gin and Tacos—just asked his readership,
What brought you here initially? Was I suggested by one of your friends? Did you arrive from a link on a different site – especially Crooks & Liars? Random internet search? Internet search specifically for gin and/or tacos? Saw a sticker on someone's car? Wrote three words in the search bar, hit ctrl-Enter, and hoped for the best?
I have been reading Gin and Tacos for almost its entire, decade-long existence. I didn't mean for that to sound so hipsterish, but there's not much other way to put it. I remember when I first stumbled on the site having entered "Robert Burnett" in my search bar, back in the days when G&T.com had more in common with its name than simply being awesome. I, like Ed, was a poor graduate student at the time, and I too had discovered the siren call of Sir Robert Burnett's London Dry Gin. (Perhaps I inherited this penchant from my advisor.)
Despite G&T.com's questionable Robert Burnett fan fiction, I was intrigued by Ed's, et al., historical sleuthing in trying to track down the truth behind the real Robert Burnett. Unfortunately, here is all they were able to conclude:
- Robert Burnett Jr. and Sir Robert Burnett were active in politics, however neither were mayor of London.
- The Burnett family was very active in military recruitment.
- Most importantly, that the Burnett family dealt in liquors.
- Finally, Sir Robert Burnett had a pretty damn nice estate.
Unfortunately, none of my research resulted in specific reference to gin. This is primarily due to the fact that the only available source to me was the Times of London, although there might have been advertisements for Burnett’s Gin in the Times, they did not come through on the search. Someone with more experience in alcohol oriented history could possibly do better.
I was no expert in history, however, like most Ph.D. students, I was a world renowned expert in procrastination. I therefore put everything else I needed to do on the back burner and took on the task. Here are my (now six year old) results:
-
John Eamer, esq. and Robert Burnett, esq. Sheriffs of London, attending his Majesty to know his pleasure concerning the city address, were honoured with knighthood.
The date that Sir Robert was knighted: Wednesday, April 15, 1795
-
CHARLES LYNN. TRIED FOR MURDER. The following are the circumstances attending a murder committed at Whaddon Chase, Buckinghamshire, in the month of 1825, which at the time of its perpetration attracted a considerable portion of the public attention." ... "A coroner's inquest was held on the body of the deceased on the following day ; and then it appeared that the prisoner was the son of a respectable woman residing at No. 4, Morehall-place, Vauxhall, where she kept a confectioner's shop, and that he, as well as the deceased, had been employed in the vinegar manufactory of Sir Robert Burnett, at Vauxhall, as coopers.
Sir Robert owned a vinegar factory. What's a common way to make white vinegar? Oxidation of distilled alcohol. I wonder where he got all of the distilled alcohol?
-
Bond, Charles, late of Gravesend, * Kent, victualler, wine and spirit merchant, d.c. Surr. Dec. 18 and 28, and Jan. 22, at 12 each day.—Sols. Messrs. Saunders and Co. Upper Thames-street. Pet. Cred. John Fassett Burnett, Vauxhall, * Surrey distiller, and Robert Burnett, and Charles Fasset Burnett, his partners. Seal. Dec. 10.
This page contains an excerpt from the London Gazette, December 11th, 1824, listing recent local bankruptcies. I’m not sure what all of the abbreviations mean, but I assume “Pet. Cred.” means “Petitioning Creditors” (i.e., the creditors to Mr. Charles Bond that are petitioning for his bankruptcy for what I can only assume as defaulting on a loan). This means that Robert Burnett is a distiller who loaned some money to a spirit merchant. Now, why would a distiller (whom we have already established as probably being quite wealthy) waste his time giving a petty loan to a spirit merchant? Perhaps he had advanced Mr. Bond some product and wished compensation?
I also found numerous primary and secondary sources speaking of the Sir R. Burnett distillery in Vauxhall. There were a few mentions of gin, but they were in books that were not freely available online.
Seven Degrees of Separation
In the year 2651 we will have to create the "Seven Degrees of Separation Game"!
Is it true that everyone on earth is separated by at most six degrees? There's plenty of empirical evidence to support this claim already, so I am going to take a different, more theoretical approach.
Béla Bollobá;s, who is famous for having studied the properties of random graphs/networks with Paul Erdős (who is himself famous, among other things, for his degrees of separation from other mathematicians), discovered loose bounds on the diameter of random regular graphs. He proved the following:
In our case, $n$ would be the world population, which we can estimate at 6.93x109. The parameter $r$ would be the minimum number of connections per person, which I think we can estimate at 130 (based on statistics from Facebook). Plugging in those values and solving for $d$ we get
This bound strictly increases as $\epsilon \rightarrow \infty$, so taking the limit as $\epsilon \rightarrow 0$ gives us the least $d$ that satisfies Theorem 1:
Therefore, by Theorem 1, the diameter of a graph on 6.93x109 vertices with degrees at least 130 almost surely has a diameter of at most 8.
According to Bollobá;s, this bound could even be sharpened (meaning that it is likely the actual value is lower than 8). The bound will of course also be tighter if people actually have more than 130 connections. Also note that this is a bound on the maximum degree of separation between people; the average degree would likely be much lower.
In summary, in a population of 6.93x109 in which each person is connected to at least 130 others, it can be said with extremely high confidence that the largest degree of separation between any two people is at most 8.
Now, at this point you might be saying to yourself: The real world social network is not a random graph! While Bollobás’s analysis does make the explicit assumption that the graph is random (which is a common tool in combinatorics), he only assumes that all graphs are equiprobable in the space of all $r$-regular graphs. That assumption is ultimately rendered moot by the strength of his result that almost all $r$-regular graphs—regardless of whether or not they are random—have this bounded diameter. The beauty is that Bollobás’s theorem applies to all (well, to be technical, “almost every”) $r$-regular graphs, not just ones that conform to the Erdős–Rényi model. In other words, we aren’t making any assumptions on the topology of the network other than its minimum degree. But there are certainly some tribal cultures that still exist that have little or no contact with the rest of the world, right? Well, let’s assume, conservatively, that there are at least 6 billion people in the population’s largest connected component. Then the bound on the degrees of separation for that largest component is still 8.
Now, on to the punchline.
If we assume that the number of connections per person, $r$, remains constant at 130, then we can set $d$ to 9 and solve for $n$ to get an estimate on the size of the population when the maximum degree of separation will increase. This will happen when the population is just under 10 Trillion. Assuming our current rate of population growth remains constant at about 1.14% per year, our population should reach 10 Trillion in about 640 years. Therefore, I conjecture that in the year 2651 we will have to create the "Seven Degrees of Separation Game"!
I’m currently teaching a class and receive all of the homework submissions digitally (in the form of PDFs). Printing out the submissions seems like a waste, so I devised a workflow for efficiently grading the assignments digitally by annotating the PDFs. My method relies solely on free, open-source tools.
Here’s the general process:
- Import the PDF into GIMP. GIMP will automatically create one layer of the image for each page of the PDF.
- Add an additional transparent layer on top of each page layer.
- Use the transparent layer to make grading annotations on the underlying page. One can progress through the pages simply by hiding the upper layers.
- Save the image as an XCF (i.e., GIMP format) file.
-
Use my
gimplayers2pngsscript (see below) to export the layers of the XCF file into independent PNG image files. - Use the composite function of ImageMagick to overlay the annotation layers with the underlying page layers, converting to an output PDF.
Below is the code for my xcflayers2pngs script. It is a Scheme Script-Fu script embedded in a Bash script that exports each layer of the XCF to a PNG file.
#!/bin/bash
{
cat < i 0)
(set! bottom-to-top (append bottom-to-top (cons (aref all-layers (- i 1)) '())))
(set! i (- i 1))
)
(reverse bottom-to-top)
)
)
(define (format-number base-string n min-length)
(let* (
(s (string-append base-string (number->string n)))
)
(if (< (string-length s) min-length)
(format-number (string-append base-string "0") n min-length)
s)))
(define (get-full-name outfile i)
(string-append outfile (format-number "" i 4) ".png")
)
(define (save-layers image layers outfile layer)
(let* (
(name (get-full-name outfile layer))
)
(file-png-save RUN-NONINTERACTIVE image (car layers) name name 0 9 1 1 1 1 1)
(if (> (length layers) 1)
(save-layers image (cdr layers) outfile (+ layer 1)))
))
(define (convert-xcf-to-png filename outfile)
(let* (
(image (car (gimp-file-load RUN-NONINTERACTIVE filename filename)))
(layers (get-all-layers image))
)
(save-layers image layers outfile 0)
(gimp-image-delete image)
)
)
(gimp-message-set-handler 1) ; Send all of the messages to STDOUT
EOF
echo "(convert-xcf-to-png \"$1\" \"$2\")"
echo "(gimp-quit 0)"
} | gimp -i -b -
Running xcflayers2pngs file.xcf output will create output0000.png, output0001.png, output0002.png, ..., one for each layer of file.xcf. Each even-numbered PNG file will correspond to an annotation layer, while each odd PNG file will correspond to a page of the submission. We can then zip the even pages with their associated odd pages using the following ImageMagick trickery:
convert output???[13579].png null: output???[02468].png -layers composite output.pdf
We can automate this process by creating a Makefile rule to convert a graded assignment in the form of an XCF into a PDF:
%.pdf : %.xcf
rm -f $**.png
./xcflayers2pngs $< $*
convert $*???[13579].png null: $*???[02468].png -layers composite $@
rm -f $**.png
Gender Representation on the Internet
In which I discover that male names appear much more often than female names on the Internet.
There is a lot that has happened since last August. I successfully defended my Ph.D., for one. I could give a report on our post-defense trip to Spain. I could talk about some interesting work I'm now doing. Instead, I'm going to devote this blog entry to gender inequity.
This all started in November of last year in response to one of Dave's blog posts. Long-story-short, he was blogging about a girl he had met; in an effort to conceal her identity (lest she discover the blog entry about herself), he replaced her name with its MD5 hash. Curious, I decided to brute force the hash to retrieve her actual name. This was very simple in Perl:
#!/usr/bin/perl -w
use Digest::MD5 qw(md5_hex);
my $s = $ARGV[0] or die("Usage: crackname MD5SUM\n\n");
system("wget http://www.census.gov/genealogy/names/dist.female.first") unless(-e 'dist.female.first');
open(NAMES, 'dist.female.first') or die("Error opening dist.female.first for reading!\n");
while() {
if($_ =~ m/^\s*(\w+)/) {
my $name = lc($1);
if(md5_hex(ucfirst($name)) eq $s || md5_hex($name) eq $s ||
md5_hex(ucfirst($name) . "\n") eq $s || md5_hex($name . "\n") eq $s) {
print ucfirst($name) . "\n";
exit(0);
}
}
}
close(NAMES);
exit(1);
Note that I am using a file called dist.female.first, which is freely available from the US Census Bureau. This file contains the most common female first names in the United States, sorted by popularity, according to the most recent census.
This script was able to crack Dave's MD5 hash in about 10 milliseconds.
This got me thinking: For what else could this census data be used?
My first idea was also inspired by Dave. You see, he was writing a novel at the time. Wouldn't it be great if I could create a tool to automatically generate plausible character names for stories?
#!/usr/bin/perl -w
use Cwd 'abs_path';
use File::Basename;
my($scriptfile, $scriptdir) = fileparse(abs_path($0));
my $prob;
$prob = $ARGV[0] or $prob = rand();
system("cd $scriptdir ; wget http://www.census.gov/genealogy/names/dist.all.last") unless(-e $scriptdir . 'dist.all.last');
system("cd $scriptdir ; wget http://www.census.gov/genealogy/names/dist.male.first") unless(-e $scriptdir . 'dist.male.first');
system("cd $scriptdir ; wget http://www.census.gov/genealogy/names/dist.female.first") unless(-e $scriptdir . 'dist.female.first');
sub get_rand {
my($filename, $percent) = @_;
open(NAMES, $filename) or die("Error opening $filename for reading!\n");
$percent *= 100.0;
my $nameval = -1;
my @names;
my $lastname;
while() {
if($_ =~ m/^\s*(\w+)\s+([^\s]+)\s+([^\s]+)/) {
$lastname = ucfirst(lc($1));
if($3 >= $percent) {
last if($nameval >= $percent && $3 > $nameval);
$nameval = $3;
push(@names, $lastname);
}
}
}
close(NAMES);
return $lastname if($#names < 0);
return $names[int(rand($#names + 1))];
}
sub random_name {
my($male, $p) = @_;
my $firstnameprob;
my $lastnameprob;
do {
$firstnameprob = rand($p);
$lastnameprob = $p - $firstnameprob;
} while($lastnameprob > 1.0);
return &get_rand($male ? 'dist.male.first' : 'dist.female.first', $firstnameprob) . " " . &get_rand('dist.all.last', $lastnameprob);
}
sub flushall {
my $old_fh = select(STDERR);
$| = 1;
select(STDOUT);
$| = 1;
select($old_fh);
}
print STDERR "Male: ";
&flushall();
print &random_name(1, $prob) . "\t";
&flushall();
print STDERR "\nFemale: ";
&flushall();
print &random_name(0, $prob) . "\n";
This script does just that. Given a real number between 0 and 1 representing the scarcity of the name, this script randomly generates a name according to the distribution of names in the United States according to the census. Values closer to zero produce more common names, and values closer to one produce more rare names. The parameter can be thought of as the scarcity percentile of the name; a value of $x$ means that the name is less common than $x$% of the other names. Note, though, that I'm not actually calculating the joint probability distribution between first and last names (for efficiency reasons), so the value you input doesn't necessarily correlate to the probability that a given first/last name combination occurs in the US population.
$ ./randomname 0.0000001 Male: James Smith Female: Mary Smith $ ./randomname 0.5 Male: Robert Shepard Female: Shannon Jones $ ./randomname 0.99999 Male: Kendall Narvaiz Female: Roxanne Lambetr
The "Male" and "Female" portions are actually printed to STDERR. This allows you to use this in scripting without having to parse the output:
$ ./randomname 0.75 2>/dev/null Gerald Castillo Christine Aaron
But I didn't stop there. Here's the punchline of this Shandy-esque recount:
Inspired by Randall Munroe style Google result frequency charts, I became interested in seeing how the frequency of names in the US correlates to the frequency of names on the Internet. I therefore quickly patched my script to retrieve Google search query result counts using the Google Search API. I generated 60 random names (half male, half female) for increasing scarcity values (in increments of 0.01). The results are pretty surprising:
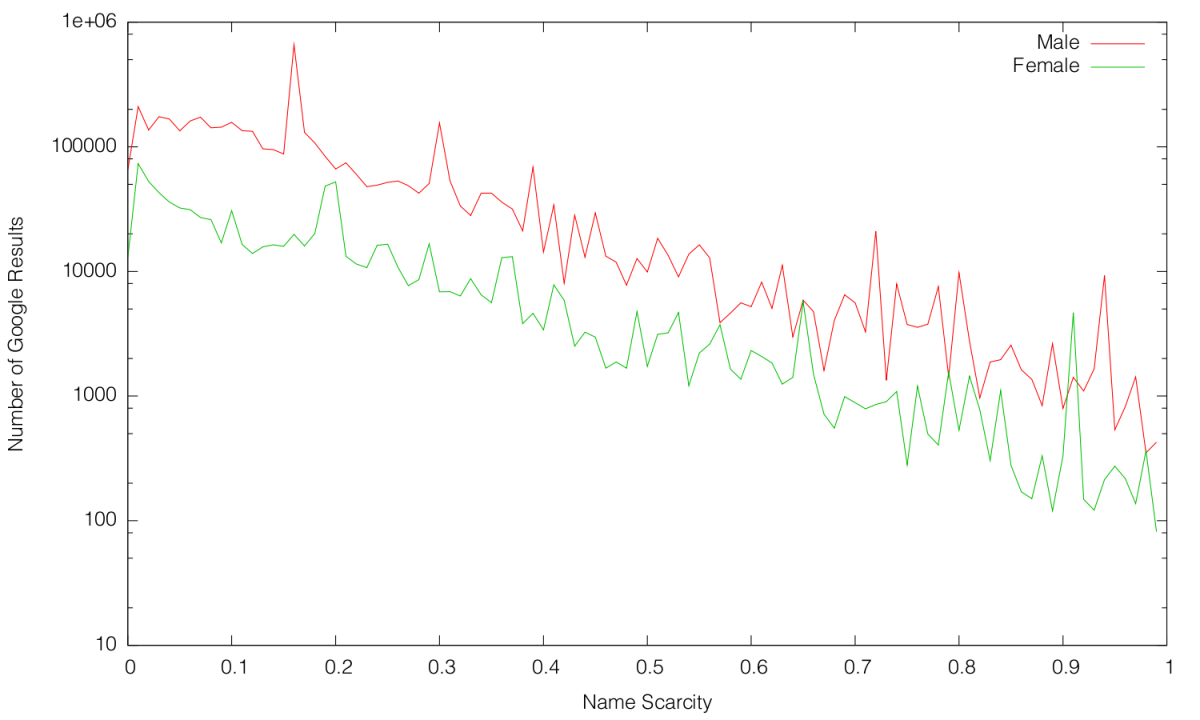
Note that the $y$-axis is on a logarithmic scale.
As expected, the number of Google search results is exponentially correlated to the scarcity of the name. What is unexpected is the disparity between representation of male names on the Internet versus female names on the Internet. On average, a male name of a certain scarcity will have over 6.6 times more Google results than a female name of equal scarcity!

Software
- Fillets from one large mackerel cut in 4cm pieces.
- 2.5cm ginger cut in matchsticks
- 2 tbsp. mirin
- 1 tbsp. sake
- 1.5 tbsp. sugar
- 1 tbsp. soy sauce
- 1 cup dashi stock (or water)
- 5 tbsp. red (“aka”) miso paste
- 2 scallions cut in 2cm pieces, whites and greens separated.
Algorithm
- Combine dashi, soy, mirin, sake, 3 tbsp. miso, and sugar in a sauce pan and bring to boil.
- Add ginger, scallion whites, and mackerel, put on tinfoil otoshi buta, and simmer on medium heat for 10 minutes, basting every few.
- Stir in remaining miso and cook for an additional 5 minutes.
- Remove from heat, add scallion greens, replace otoshi buta, and cool to room temperature in pan.
Although they are not Azeri, my wife and her family lived in Bakı from the mid-1980s through the first half of the Nagorno-Karabakh war (my father-in-law, a Colonel in the Soviet Army, was stationed there). During that time my mother-in-law developed both an appreciation for and ability to cook Azerbaijani cuisine. One dish that became my wife's favorite is called "Азербайджанский соус" (Pronounced: /ˌæzərbaɪˈdʒɑːnskʲɪj sos/ Translit.: Azerbaidzhanskiy sous, English: Azerbaijani sauce). Sous, when pronounced by a Russian, sounds like the English word "so" with an "s" consonant added at the end. It is more of a stew than a sauce, at least in my mother-in-law's interpretation. The main ingredients include eggplant, peppers, tomato, cilantro, and a whole chicken. Given that my mother-in-law's rendition is so delicious, I wanted to learn how to reproduce it in my own kitchen. Having mastered the art of cookery through observation, my mother-in-law—like most other old world home cooks—is not a woman of weights and measures; her recipes are conveyed in units of "pinches of this" and "splashes of that." This makes reproducing a dish in foreign kitchens quite difficult. One of the problems with finding a formal, written recipe for Sous is that the same word has many other meanings in French with respect to gastronomy (e.g., "Sous-chef" and "Sous-vide"), which makes Google searches (even in Russian) ripe with false-positives. Furthermore, I can't seem to find any English-language recipes. For all of these reasons, I set out to grok my mother-in-law's method. I think I have converged upon a fairly stable recipe (with some of my own modifications) which I have outlined below. In doing so, I have tried to highlight the changes I have made to the original recipe.
Hardware
- 1 heavy bottomed pot, preferably a dutch oven.
- Paper towels.
- 1 colander.
Software
- Olive oil. Clarified butter (ghee) would be more traditional, though.
- 1 large eggplant, peeled and cut into 2cm cubes.
- Kosher salt.
- 1 whole chicken, 1.5–2 kg., broken down into breasts (halved; kitchen shears work well for this), thighs, drumsticks, wings (halved at the joint), neck and back bone. My mother-in-law doesn't remember if the Azeris traditionally skin the chicken first, but she does, and I tend to agree; given that the chicken will essentially be braised, any skin would just end up being rubbery. I don't skin the wings, though, because that is a pain. Also, I would recommend brining the chicken since both the white and dark chicken meat will be cooked for equal periods. If that requires too much time/effort, you can simply buy Kosher or Halal chicken (which, by virtue of their processing, are essentially brined).
- 1 large onion, diced.
- 1 large red bell pepper, diced.
-
1 large clove of garlic, grated. My mother-in-law doesn't use this.
Garlicks, tho' used by the French, are better adapted to the uses of medicine than cookery.
—''American Cookery'' (1796) by Amelia Simmons - 1 tsp. dried, powdered turmeric. My mother-in-law doesn't use this, and I am not sure if it is traditional in sous. My Iranian Ph.D. advisor tells me that, in Persian cooking (which, neighboring Azerbaijan, is somewhat similar), turmeric is always added to onions when they are cooked.
- ~1/2 kg. potatoes (preferably red waxy potatoes, but Yukon Gold will also work), cut into 2cm cubes or wedges, equal to about 6 medium potatoes. My mother-in-law rinses the cut potatoes to remove some of their starch; I don't think this is necessary, as the small bit of starch will help thicken the stew.
- 2 large, ripe tomatoes, sliced into 5mm thick discs. Preferably skinned, but that is not critical. Roma would be a good variety, but they tend to be small so you will need more like three or four. Alternatively, I've found that you can use one 14oz. can of diced tomatoes (drained), but it would not be traditional.
- 1/3 cup cilantro, roughly chopped.
- 1 tbsp. dill, chopped.
Algorithm
Note: My mother-in-law cooks all of the ingredients separately, in separate pans, before layering everything together in the large pot for stewing/braising. While this technique may be traditional, I don't really understand its purpose. In addition to the fact that cooking everything in a single pot makes cleanup much easier, all of the fond that accumulates on the bottom of the pot remains in the stew, adding flavor from the Maillard reactions. Therefore, I just cook everything in a single enameled, cast iron dutch oven.
- Liberally salt the cubed eggplant and set aside.
- Put the dutch oven over medium-high heat and add enough fat (oil/ghee) to coat the bottom (about 1 tbsp.)
- Dry the chicken completely with paper towels. This is a lot easier if you do not wash your meat.
- Salt the chicken. If you are not using brined/treated/Kosher/Halal chicken, you will need to use a lot more salt.
- When the oil is shimmering, add the chicken. You will probably need to do the chicken in batches; you do not want to overcrowd the pan. Brown the chicken, about 1 minute on each side. Evacuate the chicken to a plate or bowl after it has browned. Add extra fat between batches, if needed.
- If there is a lot of fat in the pot, remove and reserve the excess such that there is only enough remaining to coat the bottom (about 1 tbsp.).
- Lower the heat to medium and add the onion. Sweat until the onion turns translucent, about 5 minutes.
- Add the red pepper. Sweat for another 5 minutes.
- Optionally add the garlicks and/or turmeric and cook until fragrant, about 30 seconds. If you want more of an Indian flavor you can also add fresh grated ginger, a teaspoon of garam masala, and a quarter teaspoon each of ground cumin, coriander, and cardamom.
- Reduce heat to medium-low (or "simmer" if your range has that setting), and add the potato in an even layer over the aromatics. (See the note below for a modification that adds the eggplant before the potato.)
- Add the browned chicken, along with any accumulated juices. Try and place the chicken in an even layer on top of the potato.
- Place the eggplant in the colander and rinse to remove salt.
- Add the eggplant in an even layer on top of the chicken.
- Add the tomato on top of the eggplant.
- Pour a tablespoon or two of the reserved oil (or olive oil, if there was no excess after searing the chicken) over everything. This is not traditional, however, my mother-in-law pan fries the eggplant before adding, so adding oil now accounts for the oil that the eggplant would have absorbed if it would have been fried.
- Cover and cook, remaining on medium-low heat, until the eggplant has released its liquid, about 20 minutes.
- Once there is enough liquid to cover the chicken, push the meat down such that it is all submerged. Bring the liquid back to a simmer, cover, and cook for an additional 45 minutes, stirring once every 15 minutes.
- Add cilantro and dill.
- Taste some.
- Think.
- Adjust seasoning.
- Eat.
Note: If I were devising this recipe, I would have layered the eggplant below the chicken. I have been told by the experts (i.e., my wife and her mother) that it would ruin everything, but I couldn't imagine how! I have tried adding the eggplant to the onion and peppers and cooked them for a few minutes before layering on the potatoes, and it has worked very well, decreasing the amount of time required for enough liquid to accumulate to submerge the chicken. I highly recommend trying that.
I have a problem. I admit it. I have a problem deleting files. In the “good times”—vi&., when I have gigabytes to spare on my hard drive—I simply don’t bother deleting temporary files. That video I encoded/compressed to MPEG? Sure, I’ll keep the raw original! Why not? Just in case I ever need to re-encode it at a higher bitrate, you see.
Inevitably, I run low on disk space months later, at which point I’ve forgotten where all of those pesky large files are living.
Enter my script, which I simply call biggest. This
script will conveniently print the $n$ biggest files that are rooted
at a given directory. Here’s an example:
. [92MB]
|- art [15MB]
| |- .svn [7MB]
| | `- text-base [7MB]
| | |- heat.png.svn-base [2MB]
| | `- SWATipaq.png.svn-base [2MB]
| |
| |- heat.png [2MB]
| `- SWATipaq.png [2MB]
|
|- os [7MB]
| `- os.pdf [3MB]
|
|- .svn [9MB]
| `- text-base [9MB]
| `- proposalpresentation.pdf.svn-base [8MB]
|
|- eas28@palm [14MB]
|- ESultanikPhDProposalPresentation.tar.gz [12MB]
|- APLTalk.pdf [9MB]
|- proposalpresentation.pdf [8MB]
`- proposalhandouts.pdf [7MB]
It is available on GitHub, here:
Through my many years of coding, I have come to this realization:
The so-called "Ballmer Peak", as it is currently understood, is but a two dimensional projection of what in reality is a higher dimensional space, vi&.,
If you've been keeping up, you know that I was attending the Ninth International Conference on Autonomous Agents and Multiagent Systems (AAMAS) last week in Toronto, Canada. The conference went really well, as did the two workshops I also attended:
- The Third International Workshop on Optimisation in Multi-Agent Systems (OptMAS); and
- The Twelfth International Workshop on Distributed Constraint Reasoning (DCR), which Rob and I co-chaired.
I presented my paper on distributedly solving art gallery and dominating set problems on Thursday. AAMAS also allows for full papers to additionally present a poster for the work. This was my first time making a poster purely in LaTeX, and it was a very smooth experience. I created a poster template for the Drexel CS department which can be downloaded here. You can view and download the presentation slides and poster for my paper here.
 PoC‖GTFO
PoC‖GTFO Twitter
Twitter LinkedIn
LinkedIn GitHub
GitHub XTerm
XTerm
 Esperanto
Esperanto
 עברית
עברית
 Medžuslovjansky
Medžuslovjansky
 Русский
Русский




