Recent Content:
Oh Linux, you’re simultaneously the source of and solution to all of my computing problems. I recently had my own version of Linux “success”.
This past Monday I was attending the Third International Workshop on Optimisation in Multi-Agent Systems on the first day of workshops at AAMAS. The conference venue (the Sheraton Toronto Centre) provided free wireless Internet through the use of a common username and password that was given to the attendees. I initially connected my phone (as I do not have a data plan that extends to Canada). This worked perfectly. Unfortunately, the wireless access points had an arbitrary limit to the number of users that could simultaneously connect with the same username. By the time I tried to connect my laptop, all of the user slots had been taken and I received an error.
I therefore did what any other person would have done: I fired up the terminal on my (jailbroken) iPhone, ran ifconfig and wrote down the MAC address of my phone’s wireless NIC (which was still surfing the Internets just fine). A simple ifconfig wlan0 hw ether ... command later, and my laptop was indistinguishable from my phone (at least to the hotel’s wireless access points). My laptop was then successfully on the Internet!
Unfortunately, Rob came along and ruined the whole thing. His laptop was similarly blocked from the Internet, and he needed to get online too. We decided to try and share my phone’s MAC address between our two laptops. Our laptops would just drop the unexpected packets, right? Right?
It all worked perfectly for the first five minutes or so, as long as we each took turns “using” the connection. When we tried to simultaneously browse the Internet, however, things started to break. You see, I am using a hacked open source version of my laptop’s wireless driver (it is the only way to get the wireless card into promiscuous mode). This driver is in BETA, at best, and was apparently not designed with the use case of MAC address sharing in mind. My kernel promptly panicked.
Now, I tend to always suspend or hibernate my laptop between uses. As such, the uptime of my laptop was nearly 50 days. Sometime during those 50 days I had apparently upgraded X. I had also apparently forgotten to upgrade the associated video and keyboard/mouse drivers for my laptop. Therefore, once I rebooted from the kernel panic, Xorg failed to load. That’s no problem; I’ve forgotten to compile the video drivers lots of times before. Since I didn’t have an Internet connection (and didn’t want to risk sharing the MAC address again), I gave Rob (who was still online) the URL for the download, and he copied the drivers to a USB key. Five minutes later and my video drivers were upgraded. Xorg starts up beautifully.
The problem is that I forgot to download and install the new input drivers, so neither my mouse nor my keyboard work when Xorg pops up! I have no way of quitting, so I am forced to power down.
Xorg is a boot service, so it automatically starts once I reboot my computer, and I have no way to prevent it from starting.
I therefore have to reboot into single user mode, have Rob copy the keyboard drivers over, and install them.
I still love Linux.
I've deliberated long and hard to decide whether or not to publish this blog entry.
I'm afraid that, given I've not yet completed my Ph.D., it will be misconstrued as boastful or, worse yet, exculpating. This is not my intention. If anything, I hope that my observations below will help others pursuing a Ph.D. to both rationalize their own situation and educate others on the process.
It's been a long while since I've posted to this blog, in large part due to the fact that I've been in the throes of wrapping up my degree and hunting for a job. As such, I get a lot of questions from non-academics as to when I will finish. It seems like many people are under the impression that a Ph.D. is "what you get if you tough it out and stay in school and study a few more years after undergrad." While this is technically true, many either don't realize or don't understand that a Ph.D.—at least in the sciences, engineering, and mathematics—requires independent research. A Ph.D. isn't earned through studying hard and passing tests. It's particularly frustrating when people see that I've been pursuing my Ph.D. for ~4 years (an average, if not short, duration for the degree) and immediately draw the conclusion that, "Since [he] hasn't graduated yet, [he] must not be studying hard enough!" Over the years, I've developed a metaphor that I give to people to explain the process:
Earning a Ph.D. is like trying to fund one's retirement through treasure hunting.
When I started my Ph.D., I had to choose a topic to study. That's like choosing a location in a vast field on which to begin digging for buried treasure. You know that the treasure is out there somewhere, but you're not sure where or how deep. This is not entirely up to chance: One's advisor(s)—experts in gold digging—do help in choosing the location, and there are ways to intelligently predict where the treasure might lie. The trouble is that one might dig for years and years and only be left with a huge pile of dirt. Worse yet, one might be only a few millimeters of soil away from the gold and not even know it. Every once in a while one might find a small nugget of gold in the dirt, egging him or her on, but there is no guarantee that one will eventually hit the mother lode. In other instances, one knows exactly where the treasure lies, but it is underneath an impenetrable rock that requires years and years of chipping away to exhume. In some cases one does find a huge treasure chest, but more often than not one's fortune is amassed from accumulation of the small nuggets. Defending one's dissertation, then, is like choosing to go into early retirement based off of one's fortune amassed from treasure hunting. Is it enough? Will I be able to support myself on what I've found so far? In order to complete one's degree, one has to defend his or her work to a committee of experts—all of whom are expert treasure hunters and, in a sense, one's competition. You have to convince them that your fortune will be enough to support yourself. And you have to do all of that without wasting too much time creating fanciful metaphors of debatable import.
- Pay for a service like MobileMe.
Problem: service fees seem like overkill, and the push E-mail would be the only benefit I’d get from it. - Wrap Gmail’s IMAP service in an exchange server. There are some paid services that do this, however, Z-Push is free (if one can host it one’s self).
Problem: the iPhone only supports a single Exchange server at a time. Therefore, I’d have to choose between getting push E-mail versus over-the-air calendar/contacts synchronization that is currently provided through Google’s own “Sync” Exchange wrapper. - Write an app that uses the new Push Notification service in firmware 3.0 to remotely push mail to the phone.
Problem: this would probably be a very lucrative solution (i.e., I’ll bet lots of people would pay a nominal one-time fee for this app), but it would almost definitely be rejected from the App Store. Furthermore, it would require me to set up a back-end server running 24/7 to push the updates. - Jailbreak the phone and write a daemon that runs in the background, connects to Google’s IMAP service, and goes into IDLE mode.
Problem: the only Apple device I own is my iPhone; how might I compile my own apps for it? (Sure, my wife does have a PowerBook, but that would be cheating, right? Right‽)
- Compile native apps (both console and Cocoa/Springboard/GUI) for the Apple iPhone.
- Utilize API features up to version 2.2.
- Do both of the above on Linux/BSD (probably also including—but not personally tested—on OSX and from Cygwin).
- Use API 3.0 features (AFAIK), however, the binaries created by the toolchain can run on iPhones running firmware 3.0 just fine.
- Submit apps to the App Store.
- Simulate the iPhone on your desktop (like XCode’s simulator).
- Install binaries to a non-jailbroken phone (AFAIK).
- You must have a subversion client installed.
- You must have a non-ancient version of Java installed.
- You need the xar and cpio utilities.
- You obviously need all of the dependencies required to compile the gcc cross-compiler (none of which I know offhand).
- Command line skillz.
$ mkdir -p ~/projects/iphone/ $ cd ~/projects/iphone/toolchain $ svn checkout http://iphonedevonlinux.googlecode.com/svn/trunk/ ./Modify
IPHONE_WIKI_KEY_URL in toolchain.sh (around line 96) to be the following:
http://www.theiphonewiki.com/wiki/index.php?title=VFDecrypt_Keys:_2.xand then run
$ chmod u+x toolchain.sh $ mkdir -p files/firmware $ mkdir -p sdksDownload the latest iPhone SDK from here (you need to have an apple developer account, which is free). This should end up being a
.dmg file. You need to get two .sdk files out of this .dmg. The toolchain.sh file has code to do this for you, but I couldn’t get it to work. Therefore, I used a free tool called hfsexplorer; download it here. It doesn’t claim to work in Linux, but it turns out that it was written in Java so in actuality it works fine. Just download the .zip version, go into the ./lib/ directory and run
$ java -jar hfsx.jarA GUI will pop up. Open the iPhone SDK
.dmg file and locate MacOSX10.5.pkg (or whatever is the latest version) in the Packages directory; extract it to the sdks subdirectory in your toolchain directory. Rename it to macosx.pkg. Also in the Packages directory, there should be a .pkg for the latest iPhone SDK. I forget what it was called, but it should be obvious (famous last words). Also extract that file to the sdks directory and rename it to iphone.pkg.
$ cd ~/projects/iphone/toolchain/sdks $ xar -xf iphone.pkg Payload $ cat Payload | zcat | cpio -id $ mv -f mv -f Platforms/iPhoneOS.platform/Developer/SDKs/iPhoneOS*.sdk . $ xar -xf macosx.pkg Payload $ cat Payload | zcat | cpio -id $ mv -f SDKs/MacOSX10.*.sdk .Now you should have two
.sdk files in the sdks dir. You can delete all other files in that directory; you don’t need them anymore.
$ cd ~/projects/iphone/toolchain/files/firmwareDownload the
.ipsw file for the 2.2.1 firmware into this directory (I haven’t yet tried this with the 3.0 firmware). You can find the .ipsw file stored within the file structure of iTunes’ Application Support directory, if you’ve ever used that version of iTunes to upgrade your iPhone to that firmware. If you don’t have it, it’s widely available online (just make sure to check the hash after you download).
Now we’re ready for the big step: compiling the toolchain!
$ cd ~/projects/iphone/toolchain/ $ ./toolchain.sh headers $ ./toolchain.sh firmware $ ./toolchain.sh darwin_sources $ ./toolchain.sh buildNow you can optionally remove some temporary files:
$ ./toolchain.sh cleanYou can test the toolchain by following the instructions here in the section of that same name, here. Good luck!
Continuing the recent theme of posting-random-scripts-as-blog-entries…
I recently needed a quick and dirty way to send a really large (~1 gigabyte) file to someone. We were both on the same LAN, so it didn’t really make sense for me to upload it to my externally hosted web server. I do not have a web server installed on my laptop and, at the time, it seemed like overkill to install a web server just so I could send him my file. Using a thumb drive or scp would have been an option, but each would require the recipient to be physically at my computer (despite being on the same LAN, he was a 10 minute walk away). Therefore, I gave myself a 10 minute deadline to code my own solution (plus it would be a fun diversion from writing my journal paper due later that day).
Given that I had a whole 10 minutes (an eternity when it comes to Perl hacking), I figured I might as well make my method generalized (i.e., not only should my script be able to send files, but it should also be able to receive).
First, I had to decide on a method. FTP seemed like a logical choice, but, besides really tech savvy people, who has full-blown FTP clients installed these days? In keeping with my generality goal, my solution would ideally be usable by, say, my mom. And moms don’t know ‘bout my FTP. Everyone, my mom (and my mom’s mom) included, has a web browser and knows how to use it. Therefore, good ol’ HTTP it was. And I even had a bunch of old code to hack together!
I ended up with a script that I call filedrop. Here’s the usage:
$ filedrop
Version: filedrop 0.1 2009-07-01 http://www.sultanik.com/
Copyright (C) 2009 Evan A. Sultanik
Usage: filedrop [OPTIONS] FILE_PATH
Options:
-s send a file by hosting it on a local web server (default)
-r receive a file by accepting it from a local web server.
FILE_PATH should be a directory to which the files should be
saved. FILE_PATH will default to '.' in this mode.
-n, --num=N quit after sending/receiving N files. If N is less than zero
the program will send/receive files until manually
terminated. If N is zero then the program will immediately
quit. Default is -1.
And here’s an example of how the file transfer went down:
LeEtH4X0r: Y0 Home Skillet! Can you fry me up some juarez‽
Me: Indubitably!
$ filedrop -s -n1 ./hugefile.tar.gz Server running at: http://my_ip:47489/Me: Go to
LeEtH4X0r: ZOMGKTHXBAI!!!!1ONE
Here’s the code:
#!/usr/bin/perl -w
use HTTP::Daemon;
use HTTP::Status;
my $version = "0.1";
my $date = "2009-07-01";
my $copyright = "2009";
my $port = 80;
sub print_usage {
print "Version: filedrop $version $date http://www.sultanik.com/\n";
print "Copyright (C) $copyright Evan A. Sultanik\n\n";
print "Usage: filedrop [OPTIONS] FILE_PATH\n\n";
print "Options:\n";
print " -s send a file by hosting it on a local web server (default)\n";
print " -r receive a file by accepting it from a local web server.\n";
print " FILE_PATH should be a directory to which the files should be\n";
print " saved. FILE_PATH will default to '.' in this mode.\n";
print " -n, --num=N quit after sending/receiving N files. If N is less than zero\n";
print " the program will send/receive files until manually\n";
print " terminated. If N is zero then the program will immediately\n";
print " quit. Default is -1.\n";
print "\n";
}
my $mode = "s";
my $num = -1;
my $last = "";
my $nextIsN = 0;
foreach my $arg (@ARGV) {
if($arg eq "-s") {
$mode = "s";
} elsif($arg eq "-r") {
$mode = "r";
} elsif($arg eq "-n") {
$nextIsN = 1;
next;
} elsif($arg =~ /-n(\d+)/) {
$num = $1;
} elsif($arg =~ m/--num=(\d+)/) {
$num = $1;
} elsif($nextIsN) {
$num = $arg;
} else {
if(!($last eq "")) {
print_usage() && die("Invalid option: " . $last . "\n");
}
$last = $arg;
}
$nextIsN = 0;
}
if($last eq "" && $mode eq "s") {
print_usage() && die("Path to a file to host expected!\n");
} elsif($last eq "" && $mode eq "r") {
$last = ".";
}
my $file = $last;
exit(0) if($num == 0);
my $d = HTTP::Daemon->new(LocalPort => $port) || HTTP::Daemon->new() || die;
print "Server running at: ", $d->url, "\n";
my $servings = 0;
while(my $c = $d->accept) {
while(my $r = $c->get_request) {
if($mode eq "s") {
if($r->method eq 'GET') {
print "Someone's downloading!\n";
$c->send_file_response($file);
print "Download finished!\n";
$servings++;
} else {
$c->send_error(RC_FORBIDDEN)
}
} elsif($mode eq "r") {
if($r->method eq 'POST') {
print "Someone is uploading!\n";
$servings++;
my $url = $r->content;
while($url =~ m/.*?-+(\d+)\r\nContent-Disposition:.*? filename="([^"]+)".*?\r\n\r\n(.*?)\r\n-+\1-+(.*)$/ism){
my $id = $1;
my $filename = $2;
my $content = $3;
$url = $4;
my $newName = $filename;
my $i = 0;
$newName = $filename . "." . ++$i while(-e $file . "/" . $newName);
if($i > 0) {
print "A file of named $filename already exists in $file!\n";
print "Saving to " . $file . "/" . $newName . " instead.\n";
$filename = $newName;
}
open(OUTFILE,">" . $file . "/" . $filename) or die("Error opening $file/$filename for writing!\n");
binmode OUTFILE;
print OUTFILE $content;
close(OUTFILE);
print "Received $filename (ID: $id)\n";
}
$h = HTTP::Headers->new;
$h->header('Content-Type' => 'text/html');
my $msg = "Uploaded Uploaded!
";
$msg .= "Click here to upload another file.
" if($num < 0 || $servings < $num);
$msg .= "";
$r = HTTP::Response->new( HTTP_OK, "", $h, $msg);
$c->send_response($r);
} elsif($r->method eq 'GET') {
print "Someone connected! Sending the upload form...\n";
$h = HTTP::Headers->new;
$h->header('Content-Type' => 'text/html');
$r = HTTP::Response->new( HTTP_OK, "", $h, "Upload ");
$c->send_response($r);
print "Sent!\n";
} else {
$c->send_error(RC_FORBIDDEN);
}
last if($num > 0 && $servings >= $num);
}
last if($num > 0 && $servings >= $num);
}
$c->close;
undef($c);
last if($num > 0 && $servings >= $num);
}
close($d);
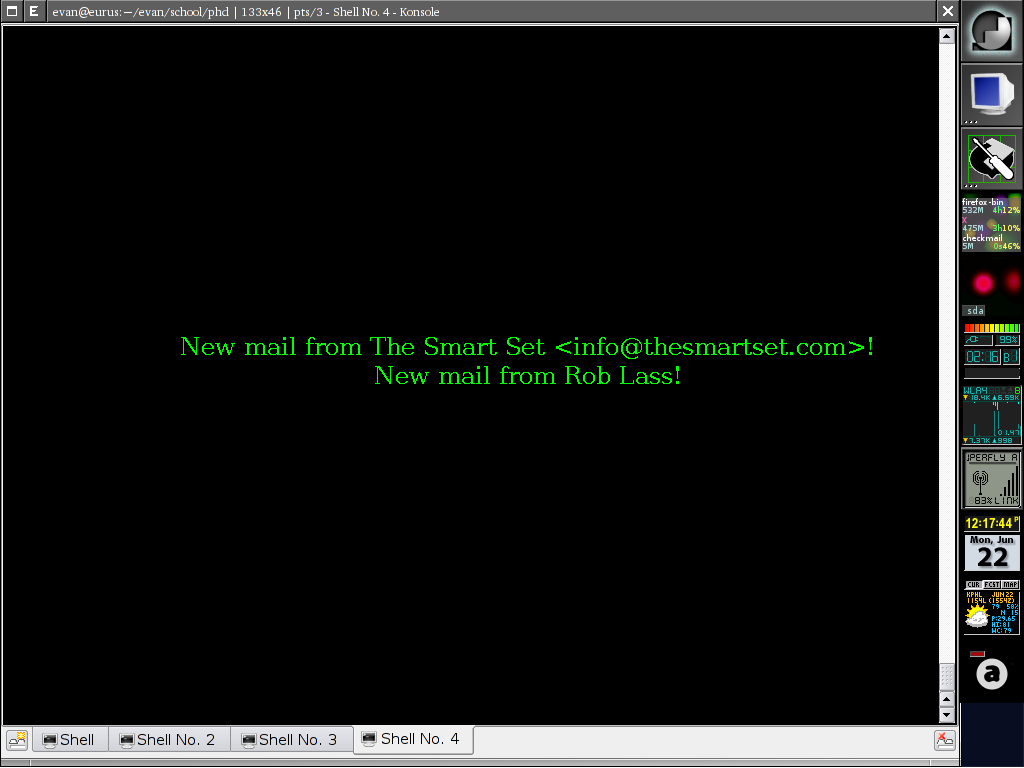
I recently caught a glimpse of how Gmail Notifier works on a friend’s Mac. It looked pretty cool. Unfortunately for me, though, there’s no reasonable facsimile in Linux. Sure, there are a couple options, but they aren’t available in Gentoo’s package management system. Given my recent experience dealing with E-mail from Perl, I figured it would be just as easy to write my own E-mail notifier as it would be to manually install these programs (along with their dependencies). I was right. I just spent the last ~20 minutes (while idling through a meeting) writing such an app. The code follows below. Its only dependency is XOSD.
Disclaimer: I blatantly cribbed some of my code from Flavio Poletti (for the MTA stuff) and Bill Luebkert (for the password input).
Future work: right now the code simply polls the mail server once every three minutes. In the future I’ll post an update that uses IMAP Idle to reduce bandwidth.
#!/usr/bin/perl -w
use Term::ReadKey; END { ReadMode ('restore'); } # just in case
use Mail::IMAPClient;
use IO::Socket::SSL;
use File::HomeDir;
my $username = '[email protected]';
my $sleeptime = 180; # Time between checks, in seconds.
my $conffile = File::HomeDir->my_home . "/.checkmail";
######################################################
$canceled = 0;
$inwhile = 0;
sub get_passwd {
# legal clear passwd chrs (26+26+10+24=86): "a-zA-Z0-9!#$%&()*+,-./:;<=> ?@[\]^";
my @legal_clear = ('a'..'z', 'A'..'Z', '0'..'9', split //,
'!#$%&()*+,-./:;<=> ?@[\]^');
my %legal_clear; foreach (@legal_clear) { $legal_clear{$_} = 1; }
$| = 1; # unbuffer stdout to force unterminated line out
ReadMode ('cbreak');
my $ch = '';
while (defined ($ch = ReadKey ())) {
last if $ch eq "\x0D" or $ch eq "\x0A";
if ($ch eq "\x08") { # backspace
print "\b \b" if $passwd; # back up 1
chop $passwd;
next;
}
if ($ch eq "\x15") { # ^U
print "\b \b" x length $passwd; # back 1 for each char
$passwd = '';
next;
}
if (not exists $legal_clear{$ch}) {
print "\n'$ch' not a legal password character\n";
print 'Password: ';
next;
}
$passwd .= $ch;
}
print "\n";
ReadMode ('restore');
return $passwd;
}
$SIG{'INT'} = 'INT_handler';
sub INT_handler {
exit(0) if(!$inwhile);
$canceled = 1;
print "\nCaught Signal; exiting gracefully!\n";
}
print "Password: ";
my $password = &get_passwd();
while(!$canceled) {
$inwhile = 1;
my $socket = IO::Socket::SSL->new(
PeerAddr => 'imap.gmail.com',
PeerPort => 993,
)
or (print STDERR "Warning: lost internet connection!\n" && next); # Perhaps we lost the internet connection?
my $greeting = <$socket>;
my ($id, $answer) = split /\s+/, $greeting;
die "problems logging in: $greeting" if $answer ne 'OK';
my $client = Mail::IMAPClient->new(
Socket => $socket,
User => $username,
Password => $password,
Uid => 1,
)
or die "new(): $@";
$client->State(Mail::IMAPClient::Connected());
$client->login() or die 'login(): ' . $client->LastError();
die("Failed authentication!\n") unless $client->IsAuthenticated();
$client->examine('INBOX') or die "Could not examine: $@\n";
my @msgs = $client->unseen or die "Could not search the inbox! $@\n";
my $last_max = -2;
if(-e $conffile) {
# Load the old largest
open(CONFFILE, "<" . $conffile) or die("Error opening " . $conffile . "\n");
while() {
my $line = $_;
$last_max = $1 if($line =~ /^\s*last_max_uid\s*=\s*(\d+)\s*$/i);
}
close(CONFFILE);
}
my $max = -1;
my @over;
for my $msg (@msgs) {
$max = $msg if $msg > $max;
push(@over, $msg) if $msg > $last_max;
}
if($max >= 0) {
open(CONFFILE, ">" . $conffile) or die("Error opening $conffile for writing!\n");
print CONFFILE "last_max_uid = " . $max . "\n";
close(CONFFILE);
}
if($last_max >= 0) {
open(OSDC, "| osd_cat -c green -p middle -A center -s 2 -l 5 -f \"-bitstream-bitstream vera serif-*-*-*-*-17-*-*-*-*-*-*-*\"");
for my $m (@over) {
my $hashref = $client->parse_headers($m, "From")
or die "Could not parse_headers: $@\n";
print OSDC "New mail from " . $hashref->{"From"}->[0] . "!\n";
}
close(OSDC);
}
$client->logout();
sleep $sleeptime;
}
I’ve been running a number of experiments recently that require a lot of computing time. “A lot” in this case being on the order of days. It would therefore be nice to have a script that would automatically E-mail me when my experiments finish, so I know to check the results. I fully expected there to be some magic shell script out there somewhere dedicated to this very purpose: sending out an E-mail when a specified process dies. Something like this:
$ ./run_experiments& [1] 1337 $ emailwhendone 1337 Awaiting process 1337's death...
As far as I can tell, however, there is no such script/program. So, as usual, I took it upon myself to write my own. The E-mailing part turned out to be a bit trickier than I had expected.
I didn’t want my script to be dependent on the existence of a local
mail server; therefore, I first tried using sSMTP. It turns out that sSMTP requires one to
hard-code the remote SMTP server address in a .conf file,
so that approach was out.
Next I tried Mail::Sendmail, however, that
module’s support for authentication is poor at best. That module also
doesn’t support SSL, so emailing through servers like Google Mail is
out.
Therefore, I finally settled on using Net::SMTP::SSL,
which unfortunately has four dependencies. Luckily for me, those
dependencies are all easily installable on Gentoo:
- dev-perl/Authen-SASL
- dev-perl/IO-Socket-SSL
- dev-perl/Net-SSLeay
- dev-perl/Net-SMTP-SSL
I call my script emailwhendone because, well, that’s exactly what it does. The code follows at the end of this post.
Disclaimer: I blatantly cribbed some of my code from Robert Maldon (for the MTA stuff) and Bill Luebkert (for the password input).
The script can be given one of two parameters: either the PID of the process for which to wait or the unique name of the process (if there are multiple processes with the same name you will need to use the PID). Right now I have the recipient E-mail address hard-coded; it should be fairly self evident from the code how to customize this. Here’s an example:
$ ./run_experiments& [1] 1337 $ emailwhendone 1337 Password for [email protected]: ******************* Waiting for process 1337 (run_experiments) to finish... The process finished! Sending an email to [email protected]... $
Here’s the code:
#!/usr/bin/perl -w
use Net::SMTP::SSL;
use Term::ReadKey; END { ReadMode ('restore'); } # just in case
my $destination = '[email protected]';
my $server = 'smtp.domain.com';
my $port = 465;
#####################################
sub usage {
print " Usage: emailwhendone [PID|PROCESS_NAME]\n";
}
my $pid = $ARGV[0] or die &usage();
my $hostname = `hostname`;
my $pidmatch = -1;
my $processmatch = "";
my @pidmatches;
open PRO, "/bin/ps axo pid,comm |" or die 'Failed to open pipe to `ps`';
while() {
if($_ =~ m/^\s*(\d+)\s+(.+)$/) {
my $matchpid = $1;
my $matchprocess = $2;
if($matchpid eq $pid) {
$pidmatch = $matchpid;
$processmatch = $matchprocess;
@pidmatches = [$matchpid];
last;
} elsif($pid =~ m/^\s*$matchprocess\s*$/) {
$pidmatch = $matchpid;
push(@pidmatches, $matchpid);
$processmatch = $matchprocess;
}
}
}
close PRO;
if(scalar(@pidmatches) <= 0) {
if($pid =~ m/^\s*\d+\s*$/) {
print "Error: no process with ID " . $pid . "!\n";
} else {
print "Error: no process named \"" . $pid . "\"!\n";
}
exit(1);
} elsif(scalar(@pidmatches) > 1) {
print "There are multiple PIDs that match this process name!\n";
for my $match (@pidmatches) {
print $match . "\t" . $pid . "\n";
}
exit(2);
}
sub get_passwd {
# legal clear passwd chrs (26+26+10+24=86): "a-zA-Z0-9!#$%&()*+,-./:;<=> ?@[\]^";
my @legal_clear = ('a'..'z', 'A'..'Z', '0'..'9', split //,
'!#$%&()*+,-./:;<=> ?@[\]^');
my %legal_clear; foreach (@legal_clear) { $legal_clear{$_} = 1; }
$| = 1; # unbuffer stdout to force unterminated line out
ReadMode ('cbreak');
my $ch = '';
while (defined ($ch = ReadKey ())) {
last if $ch eq "\x0D" or $ch eq "\x0A";
if ($ch eq "\x08") { # backspace
print "\b \b" if $passwd; # back up 1
chop $passwd;
next;
}
if ($ch eq "\x15") { # ^U
print "\b \b" x length $passwd; # back 1 for each char
$passwd = '';
next;
}
if (not exists $legal_clear{$ch}) {
print "\n'$ch' not a legal password character\n";
print 'Password: ', "*" x length $passwd; # retype *'s
next;
}
$passwd .= $ch;
print '*';
}
print "\n";
ReadMode ('restore');
return $passwd;
}
print "Password for " . $destination . ": ";
my $password = get_passwd();
sub send_mail {
my $subject = $_[0];
my $body = $_[1];
my $smtp;
if (not $smtp = Net::SMTP::SSL->new($server,
Port => $port,
Debug => 0)) {
die "Could not connect to server.\n";
}
$smtp->auth($destination, $password)
|| die "Authentication failed!\n";
$smtp->mail($destination . "\n");
$smtp->to($destination . "\n");
$smtp->data();
$smtp->datasend("From: " . $destination . "\n");
$smtp->datasend("To: " . $destination . "\n");
$smtp->datasend("Subject: " . $subject . "\n");
$smtp->datasend("\n");
$smtp->datasend($body . "\n");
$smtp->dataend();
$smtp->quit;
}
print "Waiting for process " . $pidmatch . " (" . $processmatch . ") to finish...";
my $done = 0;
do {
$done = 1;
open PRO, "/bin/ps axo pid |" or die 'Failed to open pipe to `ps`';
while() {
if($_ =~ m/^\s*$pidmatch\s*$/) {
$done = 0;
last;
}
}
close PRO;
sleep(1);
} while(!$done);
print "The process finished!\nSending an email to " . $destination . "...";
&send_mail('Process ' . $pidmatch . ' (' . $processmatch . ') on ' . $hostname . ' finished!', 'It\'s done!');
print "\n";
I’ve now been using Twitter for about six months. While Twitter’s minimalism is no doubt responsible for much of its success, I often pine for some additional social networking features. High up on that list is a simple way of representing my closest neighbors—perhaps through a visualization—without having to manually navigate individual users’ following/followers pages. A well designed representation could be useful in a number of ways:
- It could expose previously unknown mutual relationships (i.e., “Wow, I didn’t know X and Y knew each other!);
- It could reveal mutual acquaintances whom one did not know were on Twitter; and
- Metrics on the social network could be aggregated (e.g., degrees of separation).
The code for TwitterGraph follows at the end of this post. The code depends on the simplejson module and also imagemagick. It uses the Twitter API to construct the network graph. You don’t need to have a Twitter account for this to work; it doesn’t require authentication. Each IP is, however, limited to 100 API calls per hour, unless your IP has been whitelisted. My script takes this into account. Each Twitter user requires three API to download their information, so one can load about 33 users per hour before reaching the rate limit. TwitterGraph saves its data, so successive calls will continue off where it previously left. Finally, TwitterGraph also calculates the PageRank algorithm).
Usage: paste the code below into TwitterGraph.py and run the following:
$ chmod 755 ./TwitterGraph.py $ ./TwitterGraph.py You have 100 API calls remaining this hour; how many would you like to use now? 80 What is the twitter username for which you'd like to build a graph? ESultanik Building the graph for ESultanik (output will be ESultanik.dot)... . . . $ dot -Tps ESultanik.dot -o ESultanik.ps && epstopdf ESultanik.ps && acroread ESultanik.pdf $ dot -Tsvgz ESultanik.dot -o ESultanik.svgz
There are also (unnecessary) command line options, the usage for which should be evident from the sourcecode.
#!/usr/bin/python
import simplejson
import urllib2
import urllib
import getopt, sys
import re
import os
class TwitterError(Exception):
@property
def message(self):
return self.args[0]
def CheckForTwitterError(data):
if 'error' in data:
raise TwitterError(data['error'])
def fetch_url(url):
opener = urllib2.build_opener()
url_data = opener.open(url).read()
opener.close()
return url_data
def remaining_api_hits():
json = fetch_url("http://twitter.com/account/rate_limit_status.json")
data = simplejson.loads(json)
CheckForTwitterError(data)
return data['remaining_hits']
def get_user_info(id):
global is_username
global calls
json = None
calls += 1
if is_username:
json = fetch_url("http://twitter.com/users/show.json?screen_name=" + str(id))
else:
json = fetch_url("http://twitter.com/users/show.json?user_id=" + str(id))
data = simplejson.loads(json)
CheckForTwitterError(data)
return data
def get_friends(id):
global calls
calls += 1
json = fetch_url("http://twitter.com/friends/ids.json?user_id=" + str(id))
data = simplejson.loads(json)
CheckForTwitterError(data)
return data
def get_followers(id):
global calls
calls += 1
json = fetch_url("http://twitter.com/followers/ids.json?user_id=" + str(id))
data = simplejson.loads(json)
CheckForTwitterError(data)
return data
last_status_msg = ""
def update_status(message):
global last_status_msg
# clear the last message
sys.stdout.write("\r")
p = re.compile(r"[^\s]")
sys.stdout.write(p.sub(' ', last_status_msg))
sys.stdout.write("\r")
sys.stdout.write(message)
last_status_msg = message
sys.stdout.flush()
def clear_status():
last_status_msg = ""
def save_state():
global history
global user_info
global friends
global followers
global queue
global username
data = simplejson.dumps([history, user_info, friends, followers, queue])
bakfile = open(username + ".json", "w")
bakfile.write(data)
bakfile.close()
def build_adjacency():
global friends
idxes = {}
adj = []
idx = 0
for user in friends:
idxes[user] = idx
idx += 1
adj.append([0]*len(friends))
for user in friends:
if len(friends[user]) <= 0:
continue
amount_to_give = 1.0 / len(friends[user])
for f in friends[user]:
if str(f) in idxes:
adj[idxes[user]][idxes[str(f)]] = amount_to_give
return [idxes, adj]
try:
opts, args = getopt.getopt(sys.argv[1:], "hu:c:r", ["help", "user=", "calls=", "resume"])
except getopt.GetoptError, err:
print err
#usage()
sys.exit(2)
max_calls = -1
username = ""
load_prev = None
for o, a in opts:
if o in ("-h", "--help"):
#usage()
sys.exit()
elif o in ("-u", "--user"):
username = a
elif o in ("-c", "--calls"):
max_calls = int(a)
elif o in ("-r", "--resume"):
load_prev = True
else:
assert False, "unhandled option"
if max_calls != 0:
# First, let's find out how many API calls we have left before we are rate limited:
update_status("Contacting Twitter to see how many API calls are left on your account...")
max_hits = remaining_api_hits()
if max_calls < 0 or max_hits < max_calls:
update_status("You have " + str(max_hits) + " API calls remaining this hour; how many would you like to use now? ")
max_calls = int(raw_input())
clear_status()
if max_calls > max_hits:
max_calls = max_hits
if username == "":
print "What is the twitter username for which you'd like to build a graph? ",
username = re.compile(r"\n").sub("", raw_input())
update_status("Trying to open " + username + ".dot for output...")
dotfile = open(username + ".dot", "w")
update_status("")
clear_status()
print "Building the graph for " + username + " (output will be " + username + ".dot)..."
is_username = True
history = {}
queue = [username]
calls = 0
user_info = {}
friends = {}
followers = {}
# Let's see if there's any partial data...
if os.path.isfile(username + ".json"):
print "It appears as if you have some partial data for this user."
resume = ""
if not load_prev:
print "Do you want to start off from where you last finished? (y/n) ",
resume = re.compile(r"\n").sub("", raw_input())
if load_prev == True or resume == "y" or resume == "Y" or resume == "yes" or resume == "Yes" or resume == "YES":
is_username = False
bakfile = open(username + ".json", "r")
[history, user_info, friends, followers, queue] = simplejson.loads(bakfile.read())
print str(len(friends)) + " friends!"
bakfile.close()
print "Loaded " + str(len(history)) + " previous Twitterers!"
print "The current queue size is " + str(len(queue)) + "."
else:
print "You are about to overwrite the partial data; are you sure? (y/n) ",
resume = re.compile(r"\n").sub("", raw_input())
if not (resume == "y" or resume == "Y" or resume == "yes" or resume == "Yes" or resume == "YES"):
exit
while len(queue) > 0 and calls + 3 <= max_calls:
next_user = queue.pop(0)
# Let's just double-check that we haven't already processed this user!
if str(next_user) in history:
continue
update_status(str(next_user) + "\t(? Followers,\t? Following)\tQueue Size: " + str(len(queue)))
if next_user in user_info:
info = user_info[next_user]
else:
try:
info = get_user_info(next_user)
except urllib2.HTTPError:
update_status("It appears as if user " + str(next_user) + "'s account has been suspended!")
print ""
clear_status()
continue
uid = next_user
if is_username:
uid = info['id']
history[uid] = True
is_username = False
user_info[uid] = info
update_status(info['screen_name'] + "\t(? Followers,\t? Following)\tQueue Size: " + str(len(queue)))
followers[uid] = get_followers(uid)
for i in followers[uid]:
if str(i) not in history:
history[i] = True
queue.append(i)
update_status(info['screen_name'] + "\t(" + str(len(followers[uid])) + " Followers,\t? Following)\tQueue Size: " + str(len(queue)))
friends[uid] = get_friends(uid)
for i in friends[uid]:
if str(i) not in history:
history[i] = True
queue.append(i)
update_status(info['screen_name'] + "\t(" + str(len(followers[uid])) + " Followers,\t" + str(len(friends[uid])) + " Following)")
clear_status()
sys.stdout.write("\n")
sys.stdout.flush()
save_state()
# Get some extra user info if we have any API calls remaining
# Find someone in the history for whom we haven't downloaded user info
for user in history:
if calls >= max_calls:
break
if not user in user_info:
try:
user_info[user] = get_user_info(user)
except urllib2.HTTPError:
# This almost always means the user's account has been disabled!
continue
if calls > 0:
save_state()
# Now download any user profile pictures that we might be missing...
update_status("Downloading missing user profile pictures...")
if not os.path.isdir(username + ".images"):
os.mkdir(username + ".images")
user_image_raw = {}
for u in friends:
_, _, filetype = user_info[u]['profile_image_url'].rpartition(".")
filename = username + ".images/" + str(u) + "." + filetype
user_image_raw[u] = filename
if not os.path.isfile(filename):
# we need to download the file!
update_status("Downloading missing user profile picture for " + user_info[u]['screen_name'] + "...")
urllib.urlretrieve(user_info[u]['profile_image_url'], filename)
update_status("Profile pictures are up to date!")
print ""
clear_status()
# Now scale the profile pictures
update_status("Scaling profile pictures...")
user_image = {}
for u in friends:
_, _, filetype = user_info[u]['profile_image_url'].rpartition(".")
filename = username + ".images/" + str(u) + ".scaled." + filetype
user_image[u] = filename
if not os.path.isfile(filename):
# we need to scale the image!
update_status("Scaling profile picture for " + user_info[u]['screen_name'] + "...")
os.system("convert -resize 48x48 " + user_image_raw[u] + " " + user_image[u])
update_status("Profile pictures are all scaled!")
print ""
clear_status()
update_status("Building the adjacency matrix...")
[idxes, adj] = build_adjacency()
print ""
clear_status()
update_status("Calculating the stationary distribution...")
iterations = 500
damping_factor = 0.25
st = [1.0]*len(friends)
last_percent = -1
for i in range(iterations):
users = 0
for u in friends:
users += 1
percent = round(float(i * len(friends) + users) / float(iterations * len(friends)) * 100.0, 1)
if percent > last_percent:
last_percent = percent
update_status("Calculating the stationary distribution... " + str(percent) + "%")
idx = idxes[str(u)]
given_away = 0.0
give_away = st[idx] * (1.0 - damping_factor)
if give_away <= 0.0:
continue
for f in friends[u]:
if str(f) not in friends:
continue
fidx = idxes[str(f)]
ga = adj[idx][fidx] * give_away
given_away += ga
st[fidx] += ga
st[idx] -= given_away
print ""
clear_status()
# Now calculate the ranks of the users
deco = [ (st[idxes[u]], i, u) for i, u in enumerate(friends.keys()) ]
deco.sort()
deco.reverse()
rank = {}
last_st = None
last_rank = 1
for st, _, u in deco:
if last_st == None:
rank[u] = 1
elif st == last_st:
rank[u] = last_rank
else:
rank[u] = last_rank + 1
last_rank = rank[u]
last_st = st
print user_info[u]['screen_name'] + "\t" + str(rank[u])
update_status("Generating the .dot file...")
# Now generate the .dot file
dotfile.write("digraph twitter {\n")
dotfile.write(" /* A TwitterGraph automatically generated by Evan Sultanik's Python script! */\n")
dotfile.write(" /* http://www.sultanik.com/ */\n")
for user in friends:
dotfile.write(" n" + str(user) + " [label=< | " + user_info[user]['name'])
if not (user_info[user]['name'] == user_info[user]['screen_name']):
dotfile.write(" (" + user_info[user]['screen_name'] + ")") dotfile.write(" |
| Rank: " + str(rank[user]) + " |
Earlier today, Joe Kopena and I once again presented our tag-team LATEX talk. Not familiar with LATEX? Why not read the Wikipedia article! It’s essentially a professional grade system for beautifully typesetting documents/books. There are various books and Internet tutorials that do a fairly good job of introducing the basics, so, in our talk, Joe and I cover some more advanced topics and also general typesetting snags that novices often encounter. We always get requests for our slides after each of our talks, so I figured I’d post them online (which is the purpose of this blog entry).
Note that the entire presentation was created in LATEX using Beamer. You may also want to read my notes on BIBTEX, which will eventually become a part of our talk. You can read some of Joe’s notes on LATEX on his personal wiki, here. Feel free to browse and/or post any of your general typesetting questions to this public mailing list.
On the Economics of Higher Education
In which I apply flimsy math and hand-waving to justify the time I've wasted in school.
There has been much “messaging on twitter” [sic] and “posting to blogs” [sic] of late regarding the economic benefit of pursuing a graduate degree in Computer Science. For example, there are claims, among other things, that a masters degree will require 10 years to earn back the income lost during study. A Ph.D. will require a staggering 50 years. Most everything I’ve read cites this article based upon Dr. Norman Matloff’s testimony to the U.S. House Judiciary Committee Subcommittee on Immigration. Curiously, the article everyone seems to cite does not itself have a bibliography. It does, however, credit “a highly biased pro-industry National Research Council committee” for calculating these numbers. Five to ten minutes of “searching on Google” [sic] and I was unable to find a report from the National Research Council corroborating such a claim. Can anyone point me to a link?
I do not dispute that these numbers may be correct; the purpose of this blog entry is to point out that, at least in the case of most with whom I’ve matriculated, it is flat out false.
Here is my (admittedly simple) mathematical model:
- $t$ is the number of years spent in school;
- $E[s_w]$ is the expected salary one would have earned if one did not attend school;
- $c$ is the net monetary cost of attending school per year, such as tuition paid, books purchased, &c. This value should also take into account any income earned during a school year (e.g., one’s stipend) and in many cases will be a negative number;
- $E[s_a]$ one’s expected salary after graduating school; and
- $n$ is the number of years one would have to work after graduating to make up for lost income.
Note that this model does not take attrition into account.
As an example, let’s say John is a Ph.D. student who, through a research assistantship, receives tuition remission and a stipend of $20,000 a year. This is quite reasonable (and actually a bit conservative according to this study). If John had not chosen to pursue a Ph.D. he would have been hired in a $65k entry level position, which is slightly on the high end. Once he has graduated (in the quite average term of five years), he expects to receive a salary of $85k which, according to this survey is on the low end. We also, however, have to account for taxes! From my own experience and from consulting virtually every graduate student I know, John will receive a refund for practically all of the money taxed from his income. Without going to school, John would be in the 25% tax bracket, with a normalized income of about $52k (taking the tiered bracketing system into account). After earning his Ph.D. John would have a normalized income of about $67k. Plugging these values into the model we get:
I think I was relatively conservative with my income estimates, and that's still a lot less time than 50 years! I plugged in my own stats/estimates into the model and I project that I will need fewer than five years (and I don't even make as much as some other students I know)! Furthermore, with a Ph.D., John has theoretically more potential for advancement/promotion. Once the 11 years are over, he will have much more earning potential than a degreeless John (assuming the market for Ph.D.s remains strong, which I don't think is a huge assumption given the lack of domestic technical/science Ph.D.s in the US right now).
People often ask me what I do or about what I am studying. Many have certain misconceptions and stereotypes that render the simple answer of “Computer Science” insufficient. For example, the vast majority of non-technical people with whom I’ve talked seem to think that learning new programming languages and writing programs are the primary areas of study for computer-related university majors. That’s like believing literature majors go to university to learn the intricacies of using pens and typewriters. In the ~7 years—and counting (gasp!)—in which I’ve been in higher education, I haven’t been taught a single programming language.
The following is an attempt on my part to answer these questions, in the hopes that I can hereafter simply refer people to this page instead of having to explain this for the thousandth time.
What is Computer Science?
The vast majority of people that call themselves “Computer Scientists” are occupied with solving problems. This raises the question: What is a problem? In this context, a problem is a language. Do I mean a language in the sense of “English,” “Russian,” or “Pig Latin?” In a way, yes. Now, let me explain.
Languages and problems
A language is really just a set of grammar rules and a set of words that constitute a vocabulary. For example, everything I’ve written so far is a part of the English language because (1) all of the sentences conform to the English grammar, and (2) all of the words of the sentences are of the English vocabulary. Although the sentence “Evan writing” contains two words that are both in the English vocabulary, the lack of a verb (e.g., “Evan is writing”) means that it does not conform with the English grammar and is thereby not an English sentence. Likewise, the sentence “Boy ball threw” is not in English because it is unclear from the word order which noun is the subject and which is the object.
It turns out that lots of real-world problems—and virtually all computational problems—can be represented in terms of languages. For example, say you want to check whether a list of numbers is sorted in order. That problem is the same as creating a language in which the vocabulary is the set of all numbers, the grammar only allows nondecreasing numbers to appear after one another, and the problem then becomes testing whether the given list is a member of that language.
The majority of the work in Computer Science is concerned with automatically and efficiently testing whether a given sentence conforms to a given language.
Example: Sudoku
Let’s consider the popular game of Sudoku. A “language” for Sudoku might consist of:
- Vocabulary: 1, 2, 3, 4, 5, 6, 7, 8, 9
- Grammar: The set of all sentences that are exactly $9 \times 9 = 81$ characters long (representing the 81 Sudoku squares) and that conform to the Sudoku property.
It’s relatively easy to test whether a given sentence conforms to the Sudoku grammar; all we have to do is make sure that the Sudoku property holds (i.e., there are no repeats in the columns, rows, or boxes). This can be done relatively quickly by a human, and almost instantaneously by a computer. A computer scientist, however, might try and solve the following problem: “Given a partially complete sentence, either complete the sentence such that it conforms to the Sudoku grammar or prove that such a completion does not exist.” Such a problem is much harder to solve.
The majority of computer science consists of creating automated algorithms that can solve such problems. The question is: how expensive is the algorithm? Since testing whether a sentence is in the grammar is easy, one might just enumerate all of the possible Sudoku grid layouts and find the first one that is a part of the grammar. The problem is that, in the worst case, there will be on the order of $9^{81} =$ 196,627,050,475,552,913,618,075,908,526,912,116,283,103,450,944,214,766,927,315,415,537,966,391,196,809 (i.e., about one Quinquavigintillion) possibilities to test! Even if a computer could test a trillion sentences per second, such an algorithm would take about 6 octodecillion years to finish (that’s 6 with 57 zeros afterward)! What we really want are what are called polynomial time algorithms.
Polynomial time
Let’s say a given problem is of size $n$. For example, our Sudoku problem would be of size $n = 3$ because the grid is composed of nine 3-by-3 sub-squares. Now let’s say we devise an algorithm (i.e., solution method) that allows us to solve any given Sudoku problem in no more than 1000 steps. That’s pretty quick! Using this algorithm a computer could solve any $n=3$ Sudoku problem almost instantaneously. Now, let’s say we get bored with $n=3$ Sudokus (since they’re so easy to solve now) and we now want to solve Sudoku problems on larger grids—say a $n=4$ Sudoku (i.e., a grid of sixteen 4-by-4 sub-squares). As I mentioned before, the number of possibilities for $n=9$ was about $9^{81}$; for $n=10$ there are on the order of $16^{16\times 16} = 16^{256} \approx 10\ \mbox{with 308 zeros afterward}$ possibilities! By most estimates that’s over three times the number of atoms in the universe! The question is: Given that our algorithm is so efficient at solving problems where $n = 3$, how fast will it be able to solve problems when we just increase $n$ by 1?
If for each increase in $n$ it turns out that the amount of time the algorithm needs to solve the problem increases by at most a linear amount, then we say the algorithm runs in polynomial time. This means that if we have a problem of size $n$ then a polynomial time algorithm for that problem will run in at most roughly $n^c$ steps, where $c$ is some constant.
Why polynomial time matters
Moore’s law states that processor speed doubles every two years. (More accurately, Moore’s law speaks of the number of components per integrated circuit.) This means that if we have a polynomial time algorithm that is able to quickly solve a problem of size $n$ on current hardware, we will only have to wait about $\log_2\left(\frac{n+1}{n}\right) c$ years until computer hardware becomes fast enough to solve a problem of size $n+1$. For most values of $n$ and $c$, that’s a very short time!
Why Computer Science isn’t just a science
Depending on one’s discipline, Computer Science is really an amalgam of mathematics, science, and engineering. One way of thinking about the various computing disciplines is in what types of problems they aim to solve. There is a whole field of “Computer Science” concerned with discovering new efficient (e.g., polynomial time) algorithms; this field is rooted in pure mathematics. Once can devise an algorithm and formally prove its computational efficiency; no “experimentation” is required.
It turns out, however, that there are some classes of languages/problems that are so hard that it is probably impossible to devise a polynomial time algorithm to solve them! Sudoku is actually one such problem. There is therefore an entire discipline within Computer Science concerned with finding algorithms that give an approximate solution whose quality is not necessarily optimal but within a close range of optimal. This field is also rooted in pure mathematics.
Then there are problems that are so complex that either no approximation can be found or, perhaps, one doesn’t even know the grammar for the problem’s language. For example, consider the game of poker. Since poker is both non-deterministic (i.e., there is chance involved) and unobservable (i.e., one doesn’t necessarily know what is going on in other players’ hands/heads), an optimal poker-playing algorithm/strategy will be a function of the other players’ strategies. How can one prove that one’s poker playing algorithm is not only efficient, but “optimal”? How does one know that it will always play well, regardless of the opponents’ strategies? Creating the algorithm may require building heuristics, which is engineering. Evaluating the algorithm requires experimentation: playing one’s algorithm against a number of opponents over a number of games and observing the outcome, which is science.
The latter field generally falls under the term “Artificial Intelligence” (AI), the definition for which I usually give being, “The creation of systems capable of finding solutions to arbitrarily difficult problems.” The practitioners of AI generally fall into two camps: the neats and the scruffies. The neats like to design systems using formal logic and mathematics; since such methods are infallible, once a method is produced then the work is done. The scruffies, on the other hand, like to engineer systems that tend to get a job done and then, retrospectively, examine the system to figure out why it worked.
I study AI and I generally fall into the “neat” camp.
 PoC‖GTFO
PoC‖GTFO Twitter
Twitter LinkedIn
LinkedIn GitHub
GitHub XTerm
XTerm
 English
English
 Esperanto
Esperanto
 עברית
עברית
 Medžuslovjansky
Medžuslovjansky

 Reply
Reply Retweet
Retweet Favorite
Favorite